
縦と横の比率が最も均斉のとれた長方形を想像してみて下さい。それは人によって様々かもしれませんが,黄金比と 呼ばれる比が最も美しいと言われています。ところで,どうしてその比率がバランスよく見えるのでしょうか。もしかしたら,その中に何か神秘的な規則が内在しているのではないでしょうか。 ここでは,それに関連するいくつかの話題を展示します。お楽しみ下さい。
1 黄金比とはなにか
歴史上,黄金比を数学の話題として初めて意識したのは,ユークリッドとされています。彼は 次のような幾何学の問題として捉えていました。
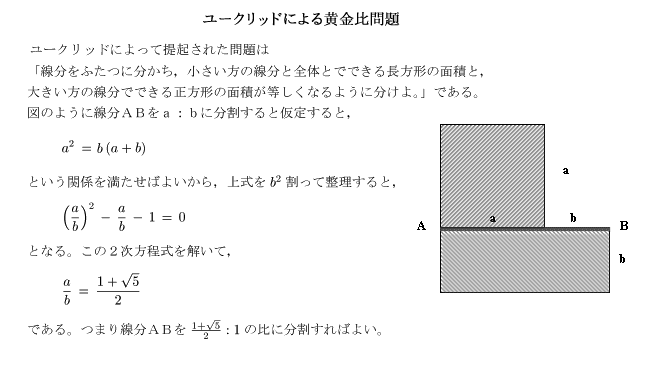
では次に,この比率を持つ長方形を作図してみましょう。
まず,1辺の長さがaの正方形ABCDを作図します。次に,辺BCの中点Mを作図し, そこからDまでの距離をとり,Mを中心に半径DMの円を描きます。 辺BCの延長線との交点をEとし,長方形ABEFを描くと,それが黄金比を持つ長方形になります。
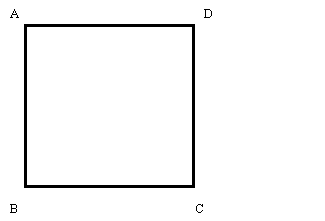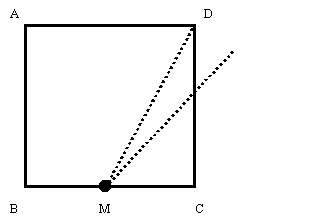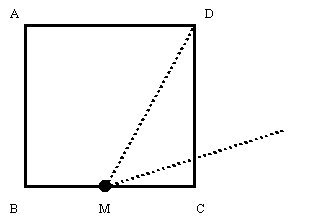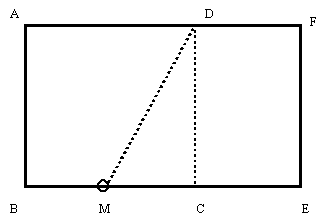

さて,この長方形がどうして均斉がとれていると見えるのでしょうか。それを探るために,その長方形の 性質を見ていきましょう。
この長方形から,最初の正方形を取り除いてできる長方形を考えます。この小さい長方形の辺の比率を計算してみましょう。
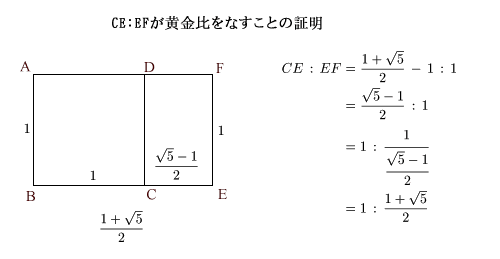
このように小さい長方形は,再び黄金比を持つ長方形です。さらに,小さい長方形から正方形を取り除いても,また黄金比を 持つ長方形が残ります。この状況は永遠に続きます。


この性質を言い換えると,この長方形は,そこから正方形を取り除いても,元の長方形と相似な長方形が残るような長方形である, と言えます。あるいは,正方形に,だんだん小さくなる正方形を付け加えていって,完全に充填できる長方形である,とも言えます。 この性質は,自然界の生物の成長の仕組みに密接に結びついています。このことから,私たち人間がそういう仕組みを内在している長方形を見るとき, 無意識のうちに,その図形を自然界を象徴した図形として受け入れているのではないでしょうか。それが,美しいという感覚を引き起こすのだろうと 想像します。
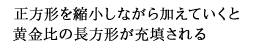

2 フィボナッチ数列と黄金比の関係
数学の世界では大変有名な,フィボナッチ数列という数の並びがあります。ここではこの数列について紹介します。
まずその数列を見て下さい。

この数列はどんな規則で並んでいるか,分かりますか。
この数列の規則は,前の2つの項の和が次の項の値になっています。この数列を始めて本格的に研究した人は,レオナルド・ピサノという 数学者(13世紀頃)ですが,彼のお父さんがボナッチという名だったので,その息子と言う意味のフィボナッチと呼ばれるようになりました(ファザー・コンプレックス だったのでしょうか)。
彼はウサギのつがいについて,「ウサギのつがいは,生まれてから2か月経つと雌雄一対の子どもを産むという。このとき,一つがいのウサギは どのように増えていくか」という問題で,この数列を研究しました。
ここではその問題を分かり易くするために,細胞分裂で言い換えてみましょう。つまり,「ひとつの子どもの細胞は1時間経つと親の細胞になり分裂可能となる。その
親細胞は,親細胞と子細胞に分裂する。この様に分裂を繰り返すと,細胞の数はどのように増えるか」という問題を考えてみましょう。
細胞の増殖の様子を1時間ごとに見ていくと,次の様になります。

細胞の数がフィボナッチ数列の数になっていくことが分かりましたか。
さて,このフィボナッチ数列と黄金比とは,どんな関係があるのでしょうか。これらはまったく似てもにつかない様に見えますが,2つの間には隠された関係があります。
それは,フィボナッチ数列の隣同士の数の比をとるとその比が次第に黄金比に近づいていく,という性質です。
つまり,フィボナッチ数列の隣同士の数の比は,黄金比の近似的な値が並んでいる,ということです。

3 自然界と黄金比について
フィボナッチ数列の生成規則は,ウサギのつがいの増加や細胞の増加の様子をうまく模倣しているように,自然界に潜むある規則を表しているように見えます。 また黄金比の性質は,美しいだけでなく,長方形の中にぴったり収まるという意味で形の上での最適な状況を表しています。これらが自然界の様々な ものの中に頻繁に見つけることができます。
ここではそのいくつかを展示します。お楽しみ下さい。
フィボナッチ数列は,草木の枝分かれの仕組みを上手く表現できます。木は,幹がある程度太くなると枝を出します。その枝もある程度太くなるとさらに枝を出します。

この様に,枝の本数にもフィボナッチ数列が現れます。
枝分かれについては,黄金比も関連しています。それは,幹の周りのどの方向に枝を出すかに関係しています。
木は自分の枝の葉が,上からの太陽光線を最大限に受けられるように,最適に枝を出す傾向にあります。
最初に出した枝から,ある一定の角度で次の枝を出すとすると,どんな角度がよいでしょうか。
それは,1周360°を黄金比に分けた角,すなわち黄金角ごとに枝をだすのが,最適であることが知られています。
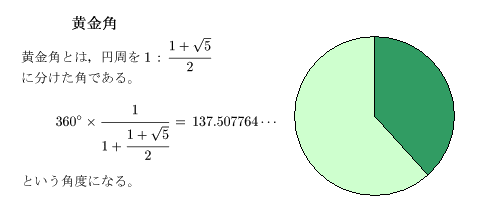
下図は,木の幹を上から見たとき枝と葉が黄金角ごとに生える様子を示しています。葉が多く茂っても,重なり合う
部分が少ないことに注目して下さい。
|
|

|
下図は,1周を3/7の比率で枝が生えていく場合をシミュレーションしています。有理数の比率の場合,何回か回ると, 重なり合ってしまい,下の葉が太陽光の陰になってしまうことを表しています。
この場合、8番目の枝が最初の枝と重なってしまいます。
|
|

|
次に,黄金角の位置で生えた芽が成長して次第に大きくなり,外側に拡がっていく様子を見てみましょう。 下の図は,木の幹を上から見たとき,外側が古い芽,内側へ行くほど新しい芽と考えて下さい。黄金角で 生えた芽は,少しずつずれながら,螺旋模様を作ることが分かります。このとき,逆向きにねじれた螺旋も微かに見えることに 注意して下さい。
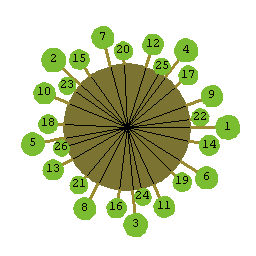

この様な植物の成長の規則が顕著に現れる実例は,ひまわり,バラなどの花の模様や松つかさの模様でしょう。



自然界の生物における現象は,その環境や進化の過程により,多種多様ですから,すべてがこの規則や性質を持つのではなく,例外はたくさんあります。 しかしその奥に潜むルールは,共通しているのではないでしょうか。
次に,螺旋模様についての例をいくつか見ていきましょう。
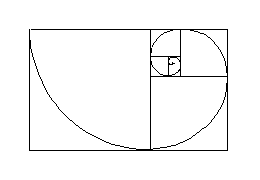
まず黄金比を持つ長方形と螺旋の関係を調べてみましょう。黄金比を持つ長方形の性質は,正方形を次第に小さくしながら加えていったときに充填される
長方形でしたので,その正方形を内側に巻き込むように配置すると,正方形が綺麗な螺旋状に並びます。
![]()
![]()

この螺旋模様を見ていると、巻き貝を連想するのではないでしょうか。ここに,巻き貝の中でも一際美しいオーム貝を展示します。
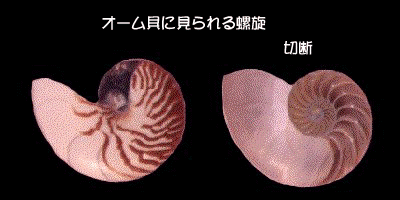
この螺旋は対数螺旋と呼ばれていて、数学的にも美しい性質を持つ螺旋です。
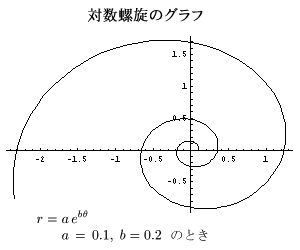
この螺旋と黄金比を持つ長方形の関係をもう少し深く見ていきましょう。
下図のように、巻き込みの点を中心に長方形を縮小しながら回転すると、常にその中に対数螺旋を内包しています。
![]()

言い換えると、黄金比に内接する対数螺旋はどこで切ってもそれに外接する黄金比を持つ長方形が存在します。ですから、対数螺旋はどこで切ってもすべて相似な曲線ということになります。
この性質は生物の形を考える上で、大変重要な意味を持ちます。生物の成長、あるいは生物の一部分の成長(爪、髪、角、甲羅など)の様子を見ていると、
少し伸びても全体としての形が変わらない様に、常に相似形を保ちながら伸びていくわけです。その伸びた部分が空間を隙間なく充填するとき、ここで見てきた様に
黄金比の長方形と対数螺旋が浮かび上がってくるのです。
4 美術と黄金比について
黄金比を持つ長方形は,最も均斉のとれた美しい長方形とされ,歴史的に古くから研究されてきました。皆さんはこの長方形を見ていると, どうして美しいと感ずるのか,考えがまとまりましたか。古今東西の芸術家は,意識的に,あるいは無意識的に,作品の中にその比率を織り込みました。

この建物の縦横の比が黄金比に近いと言われています。 |
|
この彫刻の身体の様々な部分に黄金比が見られ、 理想的な均斉美を持っていると言われています。 |
|
この絵には、螺旋の大胆な構図が見られます。 |
これらの作品にも黄金比が隠されています。
さて次に、黄金比を美しいと感ずる理由について考えてみましょう。
人間は自然を見たとき,それを美しいと感じます。そして自然の中にある均斉美に憧憬の念を禁じ得ません。
自然の中にはたくさんの黄金比が存在しています。芸術作品の中にそれらを見出すとき,人工物である芸術の印象と自然の造形の印象が等価である,という安堵感が美しいと感ずる所以なのではないでしょうか。アリストテレスの「芸術は自然を模倣する」という言葉や,セネカの「あらゆる芸術は自然の似絵である」という言葉は有名ですが,これらはそのような意味のことを言っているのではないでしょうか。
さて最後に,黄金比を持つ長方形による極めつけの芸術(?)をお目にかけましょう。この作品はすべて黄金比を持つ長方形で埋められています。その大きさはでたらめのように
見えますが,実はあの円周率(3.141592・・・)の各桁の数字で拡大縮小してあります。緑色の濃さもその値に合わせて濃淡が異なります。

|


この作品の芸術的評価は皆さんにお任せしますが,何とも不思議な模様になりました。このように並べてみて初めてわかったのですが,2が縦に連続的に並ぶ部分がありますが, 偶然の為せる技です。
以上,黄金比と美的センスについての様々な関わり合いを見てきましたが,最後に黄金比の数字としての美しさを紹介します。
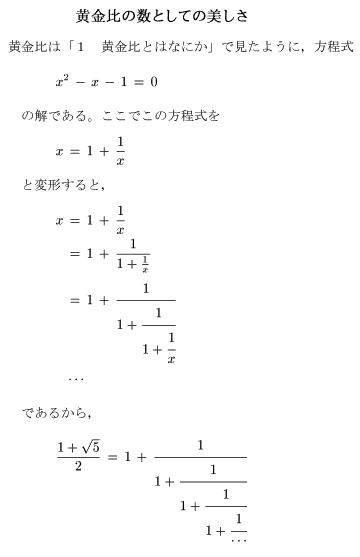

この様に,黄金比は最も単純な形をした自己相似形表現ができる数である,という意味で最も美しい数です。
5 コンピュータ・アルゴリズムと黄金比について
アルゴリズム(algorithm)というのは算法と訳されていますが,解法への手順ということです。黄金比はアルゴリズムの世界の中で,特に探索の場面で重要な役割を果たしています。
例えば,1本道の地下に埋設された水道管のどこかに穴が空いて水漏れがしている,とします。そこはAB区間内にあることは分かっていますが,その何処なのかは分かりません。そこで 観測点Pの地面に好感度のマイクを当てて水漏れの音を聞きながら,穴の場所を特定していきます。マイクは工夫がされていて,穴の場所がその地点のA側にあるのか,B側にあるのかが分かります。 もしA側にあるなら,区間PAで同様の測定をし,だんだんと区間を狭めていきます。
さてこのとき,どのような地点で調査すれば最も速く穴の場所が特定できるでしょうか。

上図のように,区間ABを黄金比に内分する視点で測定し,次に水漏れのある側をさらに黄金比の内分していきます。この様に区間を狭めていくと,最も最小の手順で目的の場所が特定できることが
知られています。
以下,工事中です!
 戻る
戻る
