たとえば、英語の単語「algorithm」を辞書で調べるとしましょう。このとき、まず「a」はアルファベットの最初だから、辞書の最初の方のページp1を開いてみます。そのページp1が、たとえば「b」ならば、それより前に在るはずです。次にその範囲内の適当なページp2を開けるでしょう。そしてそのページが、たとえば「ac・・」であれば、「algorithm」は、p1とp2の間に在るはずです。このように目標の単語に向かって、ページの範囲を絞り込んでいき、ついには目標と単語を見つけることができます。
この例のように、「探索」とは、ある区間内の目標物を、いくつかの情報を頼りに区間を縮小しながら、絞り込んでいく手法です。この手法は様々な方法が考案されていて、探す状況によって使い分けられています。ここでは、その手法の基本的なアルゴリズムとして、2分法と黄金分割法を紹介しましょう。
2分法は私たちにとって最も馴染み深い方法でしょう。
2分法とは、区間を丁度半分に分けたとき、目標物がそのどちらに属するかが判断できるとき、その範囲をさらに半分にしていく、これを繰り返す方法です。この方法のポイントは「目標物がそのどちらに属するかが判断できるとき」に大変有効な方法であり、しかも大変単純な方法です。上記の辞書も2分法に近い方法です。正確に言うと、2分法と感覚的比例配分の併用です。
では、次の例で2分法を体感してみて下さい。
【例1】「2次関数の最小点(最小値を与える点)を2分法で探す。」
[0,1]区間内に2次関数の最小値(頂点)があるとします。私たちはもちろん2次関数の式は分かっていません。任意の点の関数値のみが入手できるとします。できる限り少ない回数で、最小点を含む区間をできる限り縮小したいわけです。
次のシミュレータでは、区間が縮小されていく過程を体験できます。
| 「2分法」による探索アルゴリズム体感シミュレータ |
|
「概要」 2次関数y=(x-a)^2の最小点 a を2分法によって探索する過程を観察する。 a(0<a<1)の値は、乱数によりその都度変更される。
「操作方法」
|
この方法は、「目標物がそのどちらに属するかが判断できないとき」に有効な方法です。例えば,「太平洋の何処が一番深いか」を探るとします。ただし、東京とロサンジェルスを結ぶ大圏航路上の点であることと、海底地形の極小値は一カ所のみ(単峰性)であるとします。このとき、たとえば真ん中の点で深さを測ったとして、その日本側に最深点があるのか、アメリカ側に最深点があるのかは判断できません。このような場合、少なくとも区間内の2点で深さを測ることが必要です。
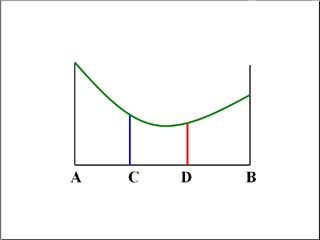
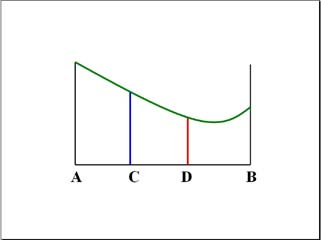
下図をみてください。
区間AB内の2点C,Dで深さ(下図の場合、関数値)を測定したとします。

|

|
赤と青の2点で測定したとき、赤の方が小さいとします。このとき、最小値の可能性は、上手のように2つありますが、いずれの場合も、その最小点は区間CB内に在ります。従って、区間をABからCBに縮小して、その区間内の2点で同様に測定します。このとき、赤の点を2点のうちの一つに選んだ方が、測定の回数を節約できますね。
この考え方による区間縮小法が、黄金分割法の根底にある考え方です。
黄金分割法は、この2点を黄金比1:(1+√5)/2と(1+√5)/2:1という内分点を利用する方法です。この方法は、測定回数が限られているとき、最も小さい区間に縮小できる方法であることが証明されています。
| 「黄金分割法」による探索アルゴリズム体感シミュレータ |
|
「概要」 2次関数y=(x-a)^2の最小点 a を黄金分割法によって探索する過程を観察する。 a(0<a<1)の値は、乱数によりその都度変更される。
「操作方法」
|
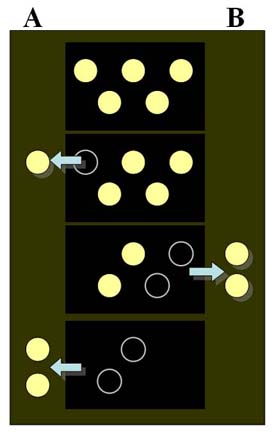
「2.フィボナッチ数列と黄金比の関係」で見てきたように、黄金比とフィボナッチ数列は密接な関係がありました。そこで、そのフィボナッチ数列が潜むゲームを紹介しましょう。 そのゲームの名前は「一山崩し」と呼ばれています。
ゲームのルールは次の通りです。
|
|
さて、このゲームの必勝法は何でしょうか。
この例の場合、実はBが次のように取れば必ず勝てます。
下に、あなたとコンピュータが対戦する「一山崩しゲーム」がありますので、挑戦して腕を磨いてみてください。
| 「一山崩し」ゲーム |
|
「概要」 あなたとコンピュータが、交互に玉を取り合います。 全部取り尽くした方が勝ちです。 相手が直前に取った玉の数の2倍まで、取ることができます。 あなたが先手です。
「操作方法」
|
以上,「黄金比のいろいろ」は終わりです。楽しめましたか!
