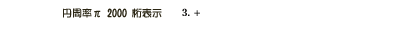
この様な方法は,古くはバビロニアや古代エジプト,古代ギリシャ,数世紀の中国など,洋の東西を 問わず試みられてきました。日本においては,関孝和もこの様な方法で近似値を求めています。
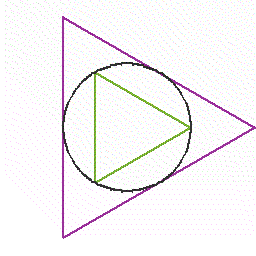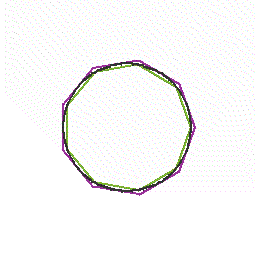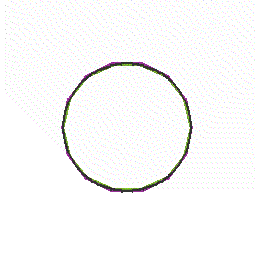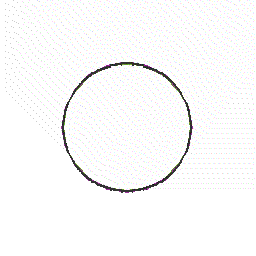
円周率をより正確にもとめる古典的な方法は,円の面積を正多角形の面積で近似していく方法でした。 円の面積がπr^2(どうしてそうなのかは,小中高と数学を勉強していくと,高校3年の微分積分の中で ,初めて納得するわけですが)ですから,r=1にすればその面積はπです。ですから, その円に内接,外接する正多角形の面積が求まれば,πの近似値が計算できます。


この様な方法は,古くはバビロニアや古代エジプト,古代ギリシャ,数世紀の中国など,洋の東西を
問わず試みられてきました。日本においては,関孝和もこの様な方法で近似値を求めています。
さて,近代,現代においては,関数を利用する方法(解析的な方法)がとられています。それはガウス(〜1855)から始まり, ニュートン,ライプニッツ,オイラーなどの業績をもとに改良が加えられてきました。ここからは専門的過ぎますので, 雰囲気だけを感じてください。

現代では円周率を計算する方法もいろいろ開発され、コンピュータを使えば原理的には時間とメモリの許す限り何桁でも求まる訳ですが、いかに速く、いかに上手く,多くの桁を計算するかが世界中で競われており、毎年その桁数の記録は更新されています。
円周率は、現在(2002年1月現在)東京大学情報基盤センターの金田康正先生によって、2061億5843万桁計算されており、これが現在世界最高記録とのことです。
これは1999年9月20日に、37時間21分04秒かかって計算さたそうです。
http://www1.coralnet.or.jp/kusuto/PI/index.html を参照してください。
ここに円周率を2000桁展示しましたので,ご覧ください。 これを見ていると,あるパターンの数字の並びが繰り返されず,「でたらめ?」に並んでいることがわかります。でも本当に そうかな,という疑問も湧いてきて,さらに先の桁が見たくなるものです。これは人間の業というものでしょうか。