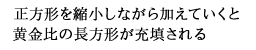1.黄金比とはなにか
1.1 黄金比の歴史
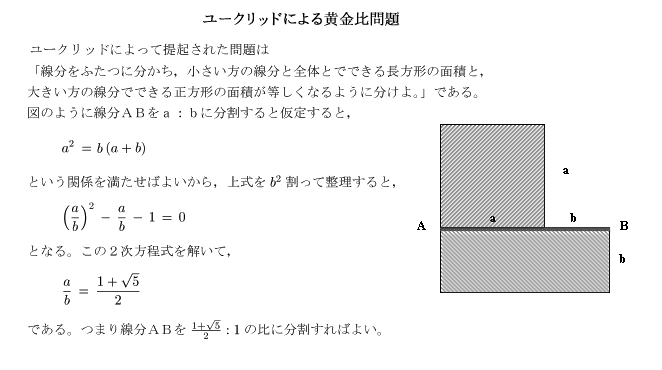
歴史上,黄金比を数学の話題として初めて意識したのは,ユークリッドとされています。彼は
次のような幾何学の問題として捉えていました。
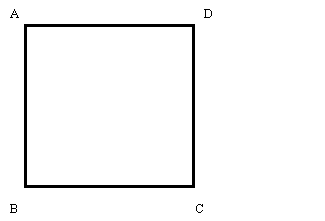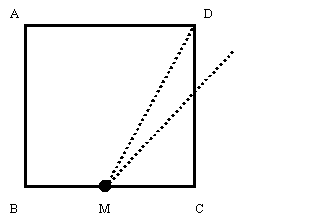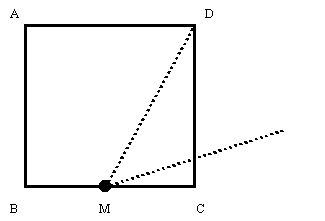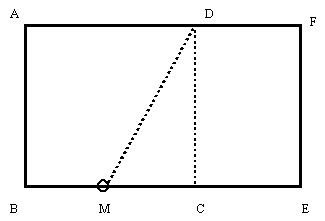
では次に,この比率を持つ長方形を作図してみましょう。
まず,1辺の長さがaの正方形ABCDを作図します。次に,辺BCの中点Mを作図し,
そこからDまでの距離をとり,Mを中心に半径DMの円を描きます。
辺BCの延長線との交点をEとし,長方形ABEFを描くと,それが黄金比を持つ長方形になります。

1.2 黄金比の均斉美
1.1で作成した長方形は、古来からもっとも均斉のとれた美しい長方形とされ、人々の意識あるいは無意識の中で、大切にされたきた図形です。
さて,この長方形がどうして均斉がとれていると見えるのでしょうか。それを探るために,その長方形の
性質を見ていきましょう。
この長方形から,最初の正方形を取り除いてできる長方形を考えます。この小さい長方形の辺の比率を計算してみましょう。
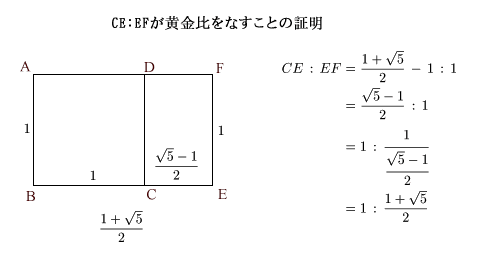
このように小さい長方形は,再び黄金比を持つ長方形です。さらに,小さい長方形から正方形を取り除いても,また黄金比を
持つ長方形が残ります。この状況は永遠に続きます。


この性質を言い換えると,この長方形は,そこから正方形を取り除いても,元の長方形と相似な長方形が残るような長方形である,
と言えます。あるいは,正方形に,だんだん小さくなる正方形を付け加えていって,完全に充填できる長方形である,とも言えます。
この性質は,自然界の生物の成長の仕組みに密接に結びついています。このことから,私たち人間がそういう仕組みを内在している長方形を見るとき,
無意識のうちに,その図形を自然界を象徴した図形として受け入れているのではないでしょうか。それが,美しいという感覚を引き起こすのだろうと
想像します。

メニューに戻る