大円が最短コースであることの説明

厳密な証明ではなく、直感的に理解しやすい説明をします。


@球面上の２点を通る様々な円を考える。

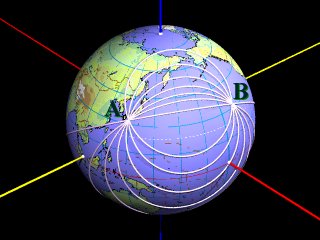
Aそれらの円を、直線ＡＢを軸にして回転し、１つの平面上に置く。

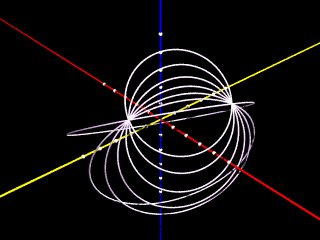
B２点ＡＢを通る円のうち、最大の円の弧ＡＢがもっとも短い。



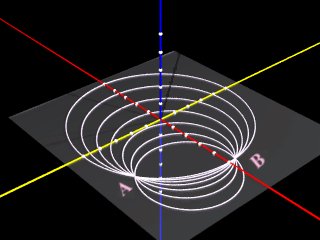
  • 弧ＡＢの長さは、円の半径が大きいほど小さくなります。
    ただし、当然のことですが、弧ＡＢは小さい方の弧（劣弧）を指します。
  • 球面上では、大円より大きな円はありません。
  • 平面上でのＡＢの最短コースは直線（線分）ですが、これは球面上にはありません。

（動画）