
俀師尦嬻娫撪偱偼丄偁傜備傞暔偑嬋柺偵増偭偰嬋偑偭偰偄傑偡偺偱丄偦偺嬋偑傝偵婥偑偮偔偙偲偼梕堈側偙偲偱偼側偄偲憐憸偱偒傑偡丅

巹偨偪偑廧傫偱偄傞悽奅偼俁師尦嬻娫偱偡偺偱丄崅偝偲偄偆奣擮偑偁傝傑偡丅
廬偭偰丄俀師尦嬻娫偺嬋柺傪丄俁師尦嬻娫撪偵昤偐傟偨恾宍偲偟偰尒傟偽丄偦偺嬋偑傝嬶崌傕堦栚椖慠偱偡丅幚嵺丄乽係丏媴柺埲奜偺戙昞揑側嬋柺乿偱丄條乆側嬋柺傪俁師尦嬻娫偐傜娤偨帇揰偱丄挱傔傑偟偨丅
偝偰丄巹偨偪偑廧傫偱偄傞俁師尦嬻娫偼丄暯傜側偺偱偟傚偆偐丄偦傟偲傕嬋偑偭偰偄傞偺偱偟傚偆偐丅傕偟嬋偑偭偰偄偨傜丄巹偨偪偼婥偑偮偔偺偱偟傚偆偐丅
偙偺媍榑偼丄乽抧媴偑暯傜側偺偐丄嬋偑偭偰偄傞偺偐乿偲偄偆恖椶楌巎忋偺媍榑偲摨偠偱偡偹丅偨偩偟丄俀師尦偑俁師尦偵曄傢偭偨偲偄偆堘偄偼偁傝傑偡丅
偙偺媍榑偡傞偨傔偵偼丄媴柺偺偲偒偵乽傑偭偡偖乿偲偄偆奣擮傪妋擣偟偨傛偆偵丄俁師尦嬻娫偱傕乽傑偭偡偖恑傓乿偲偄偆偙偲傪嵞妋擣偟側偗傟偽側傝傑偣傫丅偦偺偨傔偵偼丄俁師尦嬻娫撪偱傑偭偡偖恑傓傕偺傪尒偮偗側偗傟偽側傝傑偣傫丅偦傟偼壗偱偟傚偆偐丅
恎嬤偱媍榑偟傗偡偄傕偺偲偄偊偽丄岝偱偡偹丅
岝偼丄俁師尦嬻娫傪丄偦偺嬋偑傝偵増偭偰乽傑偭偡偖乿偵嵟抁僐乕僗傪恑傒傑偡丅
偙偺惈幙傪棙梡偟偰丄巹偨偪偺廧傫偱偄傞俁師尦嬻娫偑暯傜側偺偐丄嬋偑偭偰偄傞偺偐偑専徹偟偰偄偒傑偟傚偆丅
偦偺曽朄偼丄
傕偟俁師尦嬻娫偑嬋偑偭偰偄傞側傜偽丄岝偼偦偺嬋偑傝偵増偭偰恑傓偺偱丄岝偑嬋偑偭偨乽嵀愓乿傪懆偊傟偽丄俁師尦嬻娫偺嬋偑傝偑傢偐傞
偲偄偆棟孅偱偡丅
巹偨偪偼岝傪嫮惂揑偵嬋偘傞弍傪抦偭偰偄傑偡丅岝偼丄堎側傞攠幙傪捠夁偡傞偲偒丄乽孅愜乿傗乽斀幩乿丂偲偄偆尰徾傪婲偙偟傑偡丅偙傟傜偺尰徾偼擔忢揑偵撻愼傒怺偄尰徾偱偡丅偙偺尰徾傪愊嬌揑偵棙梡偟偨傕偺偑儗儞僘傗嬀側偳偱偡丅
偝偰偙偙偱偼丄儗儞僘偵傛偭偰岝傪恖岺揑偵嬋偘偰丄偦偙偱婲偙傞尰徾傪娤嶡偟偰傒傑偡丅偦偟偰丄傕偟丄攠幙偺側偄恀嬻偺俁師尦嬻娫偱丄偡側傢偪峀戝側塅拡嬻娫偱丄摨條偺尰徾偑娤應偱偒傟偽丄偦偺嬻娫偑嬋偑偭偰偄傞偙偲偺乽嵀愓乿偲懆偊傞偙偲偑偱偒傑偡丅偡側傢偪儗儞僘偵傛傝丄峀戝側塅拡偵偍偗傞俁師尦嬻娫偺嬋偑傝傪媈帡懱尡偟偰傒傛偆丄偲偄偆傢偗偱偡丅
偱偼憗懍傗偭偰傒傑偟傚偆丅
傑偢丄惵嬍偲丄偦傟傛傝彮偟彫偝偄愒嬍傪梡堄偟傑偡丅愒嬍偼惵嬍偺岦偙偆偵抲偒丄帇揰偐傜偼尒偊側偄傛偆偵偟傑偡丅
偝偰丄尒偊側偄偼偢偺愒嬍傪丄儗儞僘傪忋庤偔巊偭偰尒偊傞傛偆偵偱偒側偄偱偟傚偆偐丅
儗儞僘偵傛偭偰丄尒偊側偄偼偢偺暔偑尒偊傞傛偆偵側傞偐丅
|
||||
| ||||
|
乮摦夋乯
|
偙偺傛偆偵丄惵嬍偺埵抲偵丄戝偒偔岝傪嬋偘傞媴宍儗儞僘傪抲偔偙偲偵傛傝丄愒嬍偐傜弌偨岝偼丄惵嬍偺廃曈偱嬋偘傜傟偰丄栚偵擖偭偰偒傑偡丅傑偨媴宍儗儞僘偺戝偒偝偵傛傝丄愒嬍偺尒偊曽傕條乆偱偡丅
偙傟偵帡偨尰徾丄偡側傢偪 乽庤慜偺惎傑偨偼惎塤偱幷傜傟偰尒偊側偄偼偢偺惎傑偨偼惎塤偑丄榗傫偱尒偊傞乿 偲偄偆尰徾偑丄峀戝側塅拡嬻娫偱偄偔偮偐娤應偝傟偰偄傑偡丅
丂丂丂仏徻嵶偼僴僢僽儖塅拡朷墦嬀偺岞奐幨恀偺僒僀僩乮http://oposite.stsci.edu/pubinfo/Pictures.html乯側偳傪嶲徠偟偰偔偩偝偄丅
峀戝側塅拡嬻娫偵偼丄惎丄惎塤丄惎娫暔幙偲丄偦偟偰恀嬻側嬻娫偑懚嵼偟偰偄傑偡丅偦偺恀嬻偺嬻娫撪偵偼丄儗儞僘偺傛偆偵岝傪孅愜偝偣傞攠幙偵摉偨傞傕偺偼懚嵼偟偰偄傑偣傫丅 偱偼丄壗偑岝傪嬋偘偰偄傞偺偱偟傚偆偐丅暔棟妛偱偼丄乽偦傟偼俁師尦嬻娫偺嬋偑傝偑偦偆偝偣傞乿偲峫偊偰偄傑偡丅
彮偟偩偗暔棟偺悽奅傪擿偄偰尒傑偟傚偆丅
俁師尦偺塅拡嬻娫偼丄暔幙偑側偄応強偱偼嬋偑偭偰偄傑偣傫丅乽嬋偑偭偰偄側偄乿偲偼尵偆傕偺偺憐憸偟偵偔偄忬嫷偱偡偹丅偟偐偟丄俀師尦嬻娫偑乽暯傜側暯柺乿偱偁偭偨偙偲偐傜楢憐偡傞偟偐偁傝傑偣傫丅傑偨偙偺偙偲偼丄乽俁師尦嬻娫揑偵丄暯傜偱偁傞乿偲偄偆尵偄曽傕偱偒傑偡丅
暔幙偑懚嵼偡傞応強偱偼丄偦偺廃傝偺俁師尦嬻娫偑榗傒傑偡丅偙偺偙偲偼丄俀師尦嬻娫偺暯傜側暯柺忋偵暔懱傪抲偔偲丄偦偺廳傒偱暯柺偑孍傓偙偲傪楢憐偟偰偔偩偝偄丅
|
|
|
| |
|
俀師尦嬻娫偼丄僩儔儞億儕儞偵媴傪抲偄偨傛偆偵丄孍傒傑偡丅
|
媴偺戙傢傝偵俀師尦墌斦傪抲偄偨偲偒
|
亂嫵巘傊偺愱栧揑忣曬亃
|
|
俀師尦嬻娫撪偺岝偼丄偙偺孍傒偺嬋偑傝偵増偭偰丄壓恾偺傛偆偵乽傑偭偡偖乿恑傒傑偡丅
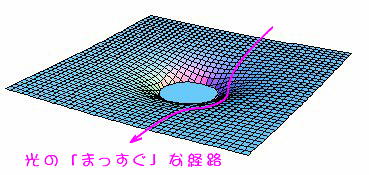
孍傒偺嬋偑傝偵増偭偰乽傑偭偡偖乿恑傓岝偺宱楬 |
俁師尦嬻娫偵廧傓巹偨偪偐傜尒傞偲丄忋偺宱楬偼柧傜偐偵嬋偑偭偰尒偊傑偡偑丄俀師尦嬻娫偵廧傫偱偄傞廧恖偐傜傒傞偲丄偙傟偑乽傑偭偡偖乿側偺偱偡丅
偙偺岝偼丄嬋偑偭偰偄側偗傟偽幷傜傟偰捠夁偟側偄埵抲偵偁傝傑偡偑丄孍傒偺嬋偑傝偵増偭偰丄乽傑偭偡偖乿恑傫偩寢壥丄栚偵擖偭偰偒傑偡丅
偄偐偑偱偟傚偆偐丅擺摼偱偒傑偟偨偐丅妋偐偵憐憸偟偵偔偄傕偺偱偡偹丅
俀師尦嬻娫偺廧恖偑丄帺暘偺廧傫偱偄傞俀師尦嬻娫偺嬋偑傝傪憐憸偡傞偙偲偼崲擄偱偡偑丄俁師尦嬻娫偐傜俀師尦嬻娫傪傒傞偲丄抧媴偺昞柺偑媴柺傪偟偰偄傞偙偲偼堦栚椖慠偱偡丅廬偭偰丄俁師尦嬻娫偺嬋偑傝偼丄係師尦嬻娫偐傜尒傟偽堦栚椖慠側偺偱偟傚偆丅乮係師尦嬻娫偵偮偄偰偼丄乽悢妛娪徿娰丂嬀偺偄傠偄傠乿傪嶲徠偟偰偔偩偝偄丅乯
埲忋丄抧媴昞柺偺榖戣偐傜弌敪偟偰丄暯柺婔壗妛偱側偄婔壗妛偺悽奅傪奯娫尒傑偟偨丅
乽嬋柺偺偄傠偄傠乿傪廔傢傞偵摉偨偭偰丄婔壗妛偺敪揥傪楌巎揑偵尒偰偄偔偲丄
恖娫偲婔壗妛偲偺偮偒崌偄偼丄乽悢乿偺奣擮偲偲傕偵桳巎埲慜偵慿傝傑偡偑丄傗偑偰婭尦慜屻偺儐乕僋儕僢僪偵傛傞婔壗妛偺廤戝惉傪宱偰丄崱擔偱偼丄暯柺婔壗妛偼儐乕僋儕僢僪婔壗妛偲偟偰惛枾偱梙傞偓側偄懱宯偑抸偐傟偰偒傑偟偨丅
偦偺夁掱偱丄拞悽埲崀丄
偝傜偵壛偊偰丄
嬻娫偺嬋偑傝偵抂傪敪偟偰丄嬻娫傪應傞偙偲偵娭楢偟偨尰戙壢妛偑乽敋敪尰徾乿偲傕尵偊傞傎偳偺敪揥傪悑偘丄偦偟偰崱傕敪揥偑懕偄偰偄傑偡丅
