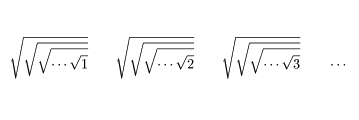
以下の例は自然数以外も出てきますが,やはり美しい並び方をしています。
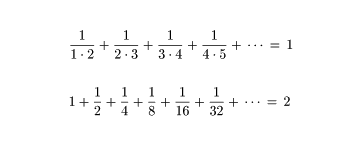
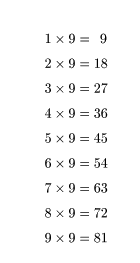
このように自然数が規則的に並んだ数を扱っていると,思わぬところで見とれてしまうような美しい数字の並びが出くることがあります。
そのいくつかを紹介しよう。


以下の例は自然数以外も出てきますが,やはり美しい並び方をしています。
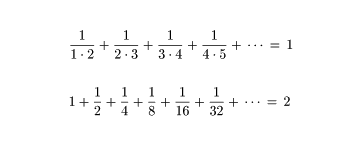
次のような並びもお洒落です。自然数1,2,3,4,5,6,7,8,9の数字をこの順に並べ,その前後に+,−を入れてちょうど100と
なる式を表しています。このような並びは全部で12通りしか在りませんが,そのうち3例を展示しておきます。残りは各自みつけてください。
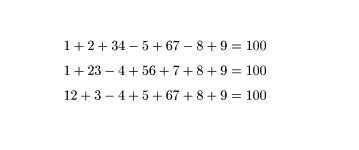
さらに×÷も使えることにすると,141通りを超えることが知られています。その一つをここに展示しますが,
全部でいくつあるのかは,まだ分かっていないようです。
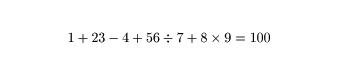
最後に,次の数はいくつでしょうか。この数は「フラクタルのいろいろ」を鑑賞すると分かるでしょう。