《混乱　�A》
「１１１１」と「１７２９（デタラメに並べた数字）」の出現確率は同じです。

このような混乱は、特別の意味のあるものとそうでないものの捉え方の問題と、それを表現する言葉の言い回しの問題に起因しています。
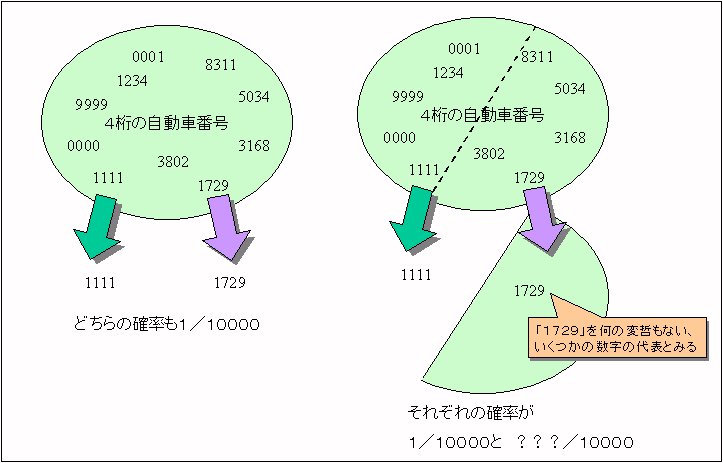
「１１１１」のように１が４つ並ぶ数字が出る確率は１／１００００なので珍しいことであり、それ以外の数字が出る確率は、１−１／１００００＝９９９９／１００００となります。（ただし、００００も含めています。）

「１７２９」という何の変哲もない数字であっても、その出現確率は、１，７，２，９の出る確率がそれぞれ１／１０ですので、やはり１／１００００です。

さて、この「１７２９」を、「１１１１」と同じように特別な数字と見ているのか、　何の変哲もない数字の「代表」　と見るかにより、議論が分かれます。要は言葉の表現とその捉え方の問題であり、それが混乱の原因です。下の図を見て下さい。

一般に、「１７２９」のような一見「何の変哲もない数字」を、「何の変哲もない数字の代表」と捉える傾向が強く、その結果、「１１１１」の方が「１７２９」より珍しい、と感じるようです。

ところで、どのような数字を特別な数字と見るかは人さまざまですね。特別な数字と何の変哲もない数字の区別は、個人的趣味の問題でもあるのでしょう。

さて、この「１７２９」 という数字は、本当に何の変哲もない数字でしょうか。皆さんは、どのように見えますか。もう一度良く見てください。特別な数字と見なしている人がいるかもしれません。

実は、この数字については「数学史上の有名な逸話」があります。 ２０世紀の初頭、インドの貧しい家庭に生まれた超天才数学者ラマヌジャンは、イギリスの大数学者ハーディーによりイギリスに招かれ、数学研究に没頭ししました。 しかし数年間の学究生活は、身体をこわす結果となり、ついに病院で死の床につくことになってしまいました。 そんなある日、ハーディーがいつものようにラマヌジャンを見舞いに来て、こう言いました。 【その時の問答】 ハーディー　：「いま乗ってきたタクシーの番号は１７２９というさえない番号だったよ。」 ラマヌジャン：「それはちがいますよ。とってもおもしろい数だ。１７２９は２つの自然数の３乗和で表すことができ、しかもそれが２通りある最小の数ですよ。」 　　　１７２９＝１０＾３＋９＾３＝１＾３＋１２＾３ ハーディー：「・・・・」 ラマヌジャンは、１９２０年に３３才の若さで病死しました。 ※（超）天才数学者について ラマヌジャンが類い希な（超）天才数学者といわれる訳は、彼が証明した膨大な公式がどれも美しいものばかりなのですが、 「それをどうやって証明したのか」、「なぜその公式が必要だったのか」などが記されておらず、 神秘のベールに包まれた数学者だからです。