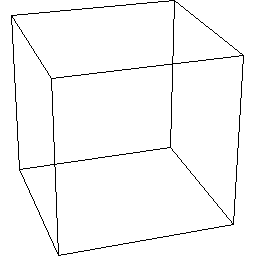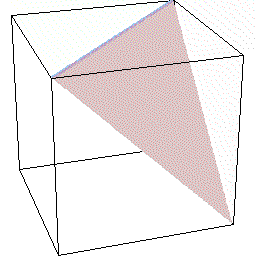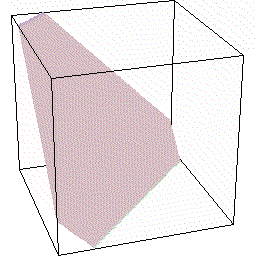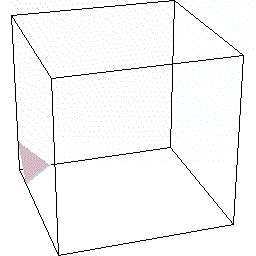
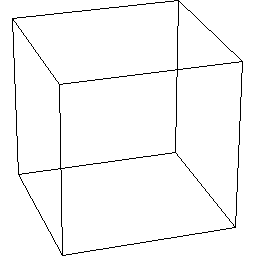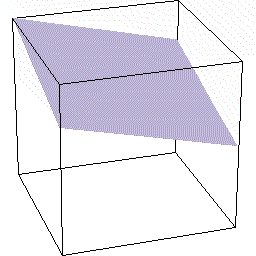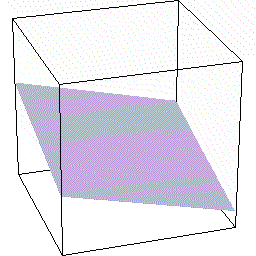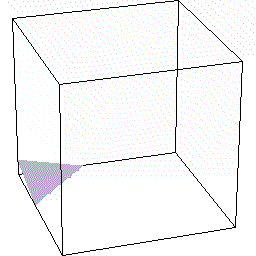
では次に合体の逆の,立体図形の切断について見ていきましょう。 この話題で最も有名な立方体の切断について取り上げます。

|

| |||
|
|
メニューに戻る

その次は立方体でしょうか,正四角錐でしょうか。正四角錐の方が頂点,辺,面の数は少ないですが,すべての面が 同じではありませんから,均斉という点では立方体が勝るかもしれません。この議論は数学の議論というよりも 美学の議論になります。
さて,単純な立体図形の間にいくつかの美しい関係がありますが,その一つを紹介しましょう。 1辺の長さが同じの正四面体と正四角錐を,合同な面で合体させたら何面体の立体ができるでしょうか。 正四面体の面は4面,正四角錐の面は5面あり,合体させて2面が合わさるので,4+5−2=7面の立体に なりそうですね。本当にそうでしょうか。
そうです!,5面体です。合体させると2組の2つの面がそれぞれちょうど平面になり,面の数が2だけ少なくなります。
では次に合体の逆の,立体図形の切断について見ていきましょう。
この話題で最も有名な立方体の切断について取り上げます。




メニューに戻る