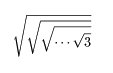
この数字の一番内側は、√３＝１．７３２０５０８・・・ですから、さらに平方に開いていくと、最終的には１になりそうですね。

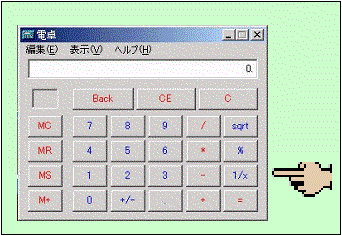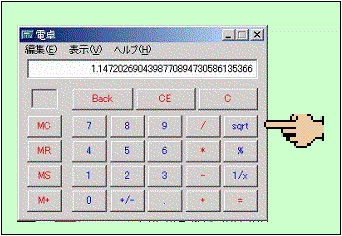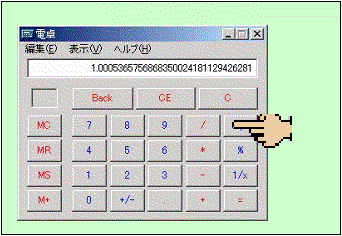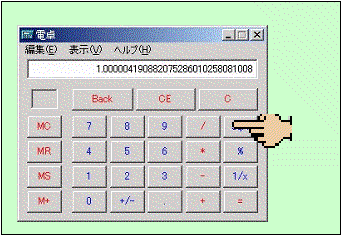
このことは、電卓を使うと簡単に実験できます。

この電卓での実験では、３のキーを叩いて√３を計算し、その後√のキーを叩いていくと、次第に１に近づいていくことが観測できます。

この過程をもう少し一般化してみましょう。

この過程は、

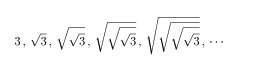
のように数字を次々に生成していきますので、「数列」の生成過程です。
すなわち、

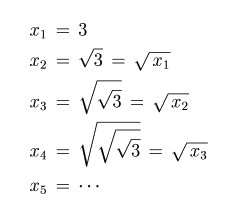
となります。
一般的に表記すると

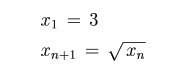
で定義される数列を生成しているわけです。

さて次に、この数列は本当に１に近づく（収束）するのか、という疑問を解決していきましょう。
ｙ＝√ｘ　のグラフ論理的証明はこのサイトの趣旨に合いませんので、グラフを利用して直感的に理解する方法を紹介します。

それは、ｙ＝√ｘ　のグラフを利用して、数列｛Ｘｎ｝（ｎ＝１，２，３，・・・）を次々にＸ軸上の点列として作図していく方法です。

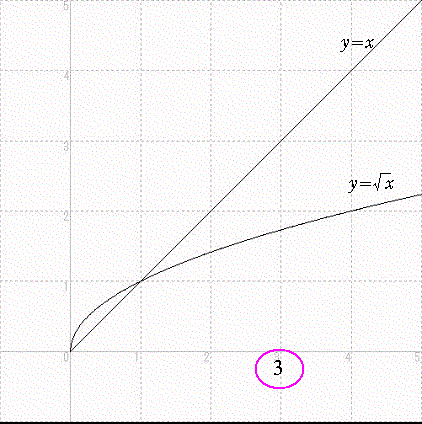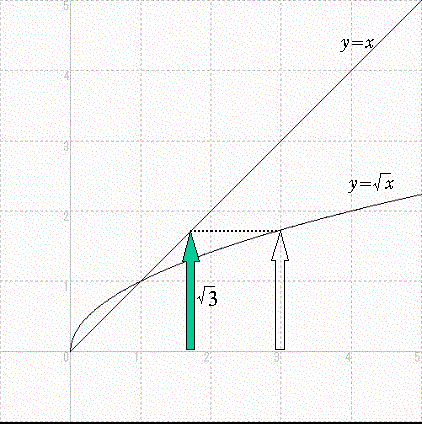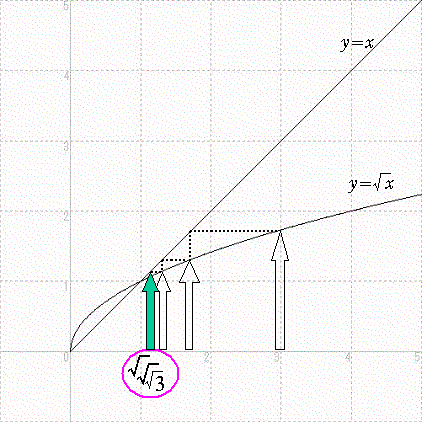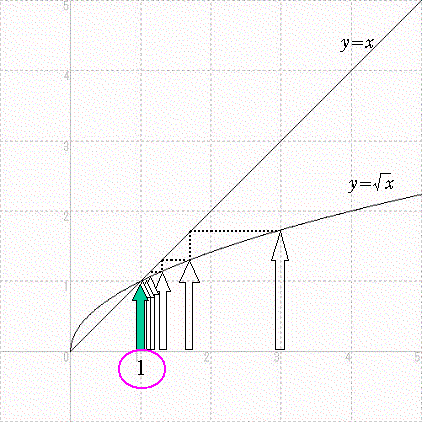
上図のように、Ｘ１＝３から始めて、ｙ＝√ｘ　のグラフから√３を読み取り、その値をｙ＝ｘ　のグラフを利用してｘ軸に移しＸ２とし、それを繰り返します。そうすると、この点列は最終的に１に近づいていくことがわかります。
ここでｙ＝ｘ　のグラフを巧みに利用していることに注目してください。

ところで，すべての数字がこの様にフラクタル構造をもっているわけではありません。 例えば無理数のπは連分数表現はできますが，内部に全く同じ形を内包してはいませんので、フラクタル構造を持つ数とはいえません。