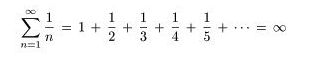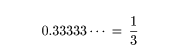
と書いても違和感はないようです。しかし,
0.3+0.03+0.003+0.0003+0.00003+・・・
でしょう。
この数字は,0.3333333・・・ですから,明らかに(本当に明らかでしょうか?)1/3であり,有限な値です。しかも
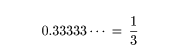
と書いても違和感はないようです。しかし,
0.99999・・・=1
については,多くの人が違和感を感じるようです。
0.9999・・・の方がほんの少し小さいような気がする人が多いのではないでしょうか。これがぴったり1であることを納得するには次のような方法が
あります。
これで納得
方法1と2は本質的には大きな違いがありませんが,方法2の方が数字の自己相似形(フラクタルのいろいろを参照)を意識した考え方です。
この様に0.9999・・・はぴったり1なのです。前者の方がやや小さいと感じるのはまさに「気のせい」です。
0.3333・・・と1/3において
前者がやや小さいと感じないのは,1/3のわり算を筆算で体験したことが利いているのだと思います。
0.3333・・・=1/3は納得しても,
0.9999・・・=1が納得できないのはやや「えこひいき」なのかもしれません。0.3333・・・の方も1/3にはやや足りないと感じる人は
極限値の意味を理解すれば腑に落ちるでしょう。それでも納得できない人は次を見て下さい。
下の計算は1÷1を積み算で計算しています。ただし,最初に1を立てるとそれで終わってしまいますので,あえて0を立てて計算します。
1÷1の積算
どうでしょうか,これで0.9999・・・=1が納得できましたか。
さて,今まで無限に数字を加えていっても有限である数を見てきました。これらの特徴は加えていく数字がだんだんに小さくなっていくような ものでした。加えていく数字がだんだんに大きくなっていくものは当然無限になります。たとえば,
1+2+3+4+5+・・・は明らかに無限(∞)
です。
ところで,加えていく数字がだんだん小さくなっていくような数字が有限であるか,無限であるか,の判断は,大変厄介であり微妙な問題です。
次の数字は有限でしょうか,無限でしょうか。
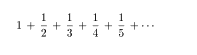
下の式は,30,000項まで加えていった和を順次表示しています。
これからわかることは,
「この和は少しずつ大きくなっていくが,その速さはとても遅い。ひょっとしたら有限の値になるかもしれないし,無限かもしれない。」
ということでしょう。実はこの数は無限に大きくなりますが,その増加が極めて遅い代表例です。このことが納得できるのは大学1年程度の数学の知識が必要です。皆さんの今後の勉強に委ねます。