偦傟偵敽偆懍搙倴乮倲乯偼丆帪懍侽倠倣偐傜帪懍俉侽倠倣傑偱曄壔偟側偑傜丆嵟廔揰偱掆巭偟傑偡丅
僌儔僼忋偱忋偲摨條偺旝暘偲偄偆憖嶌傪偟偰傒傑偟傚偆丅
|
攦偄暔偵帺摦幵偱弌偐偗偨俙偝傫偼丆惂尷懍搙偑帪懍係侽俲倣偺摴傪帪懍俇侽倠倣偱憱偭偰偄傑偟偨丅 偡傞偲僷僩僇乕偵惂巭偝傟偰丆偍弰傝偝傫偵拲堄傪庴偗傑偟偨丅乽偙偺摴偺惂尷懍搙偼帪懍係侽倠倣偱偡傛丅 偁側偨偼崱帪懍俇侽倠倣偱憱偭偰偄傑偟偨偺偱堘斀偱偡丅乿
偡傞偲俙偝傫偼乽偦傫側偼偢偼偁傝傑偣傫丅巹偼壠傪弌偰傑偩俆暘偟偐偨偭偰偄傑偣傫丅乿 |
帺摦幵偵偼懍搙寁偑晅偄偰偄偰丆崗乆偺懍搙傪昞帵偟偰偄傑偡丅偝偰丆懍搙偲偄偆傕偺偼乵堏摦偟偨嫍棧乶乛乵偐偐偭偨帪娫乶偱寁嶼偟傑偡偑丆
弖娫偺懍搙偼偳偆傗偭偰應傞偺偱偟傚偆偐丅
忋偺彫欜偺傛偆偵丆侾帪娫宱偭偰係侽倠倣堏摦偡傟偽帪懍係侽倠倣偱偁傞偙偲偼柧敀偱偡偑丆偁傞弖娫偵
帪懍係侽倠倣偱偁傞丆偲偄偆偙偲傪棟夝偡傞偵偼庒姳偺弨旛偲偦傟側傝偺庤弴偑昁梫偱偡丅偙偙偱偼偦偺庤弴傪峫偊偰傒傑偟傚偆丅
壓偺傾僯儊乕僔儑儞傪偛棗壓偝偄丅帪崗倲亖侾侽昩偵偍偗傞懍搙傪媮傔傞偵偼師偺傛偆側庤懕偒傪偟傑偡丅
|
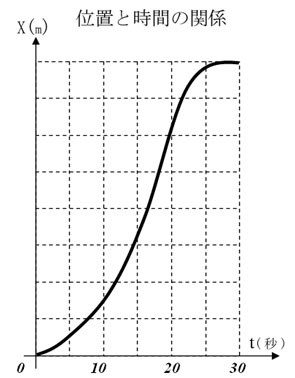
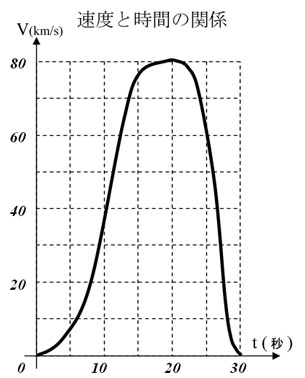
帺摦幵偺埵抲倶偼弌敪揰偐傜嵟廔揰偵岦偐偭偰帪娫偲嫟偵曄壔偟偰偄偒傑偡偐傜丆帪娫偺娭悢偲偟偰倶乮倲乯偲彂偔偙偲偵偟傑偡丅
偦傟偵敽偆懍搙倴乮倲乯偼丆帪懍侽倠倣偐傜帪懍俉侽倠倣傑偱曄壔偟側偑傜丆嵟廔揰偱掆巭偟傑偡丅


僌儔僼忋偱忋偲摨條偺旝暘偲偄偆憖嶌傪偟偰傒傑偟傚偆丅
|
|
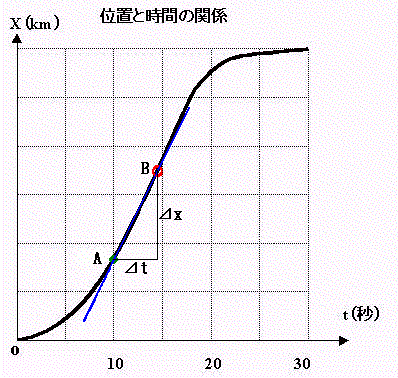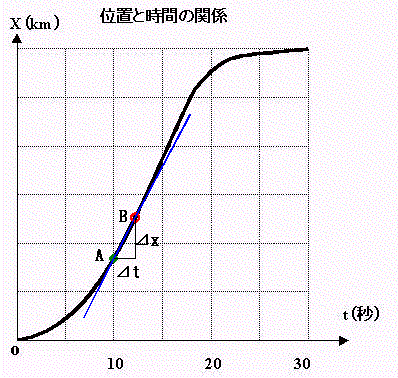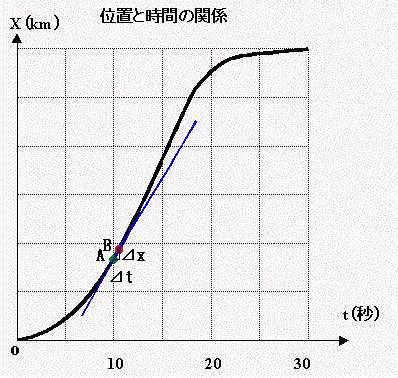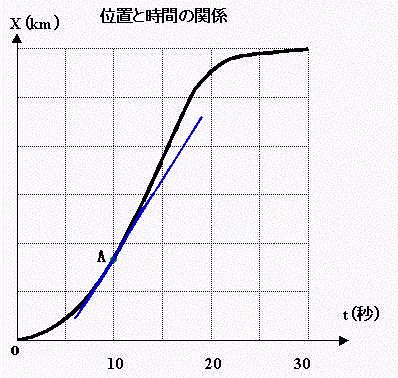
傑偲傔傞偲丆
帪崗倲亖侾侽昩偱偺弖娫偺懍搙偼丆埵抲傪昞偡娭悢偺俙揰偱偺愙慄偺孹偒傪昞偟偰偄傞 偲偄偆偙偲偱偡丅
偝偰偙偙傑偱偔傞偲丆僛僲儞偺媡愢乽旘傫偱傞栴偼巭傑偭偰偄傞乿偺摎偊偑尒偊偰偒偨偺偱偼偁傝傑偣傫偐丅
弖娫偲偄偆堄枴偼丆偦偙偱偼帪娫偺娫妘偼侽偱偡偑丆弶傔偐傜侽偱媍榑傪偡傞偺偱偼側偔丆巄掕揑側 壖憐偺娫妘嚈倲傪憐掕偟偰媍榑偟丆偦偺嚈倲傪尷傝側偔侽偵嬤偯偗偨嬌尷偱傕偭偰弖娫傪棟夝偟偰偄傑偡丅
廬偭偰丆帺摦幵傕栴傕摦偄偰偄傞傕偺偼丆偦偺弖娫偵偍偄偰懍搙傪帩偭偰偄傑偡丅
偙偺忬嫷傪乽摦偄偰偄傞乿偲偄偆偺偐丆乽惷巭偟偰偄傞乿偲偄偆偺偐偼丆尵梩偺掕媊偺栤戣偵側傝傑偡偐傜寉乆偟偔偼寢榑偱偒傑偣傫丅偟偐偟
嬌尷偺憖嶌傪椆夝偟偨忋偱偼丆弖娫偵偍偄偰傕摦偄偰偄傞
偲峫偊偨曽偑傛偄偲巚偄傑偡丅乮悢妛偱偼乽柍尷彫偺帪娫娫妘偵柍尷彫偺堏摦偑偁傞乿丆偲偄偆傛偆側棟夝偺巇曽傪偡傞偙偲偑偁傝傑偡丅乯
