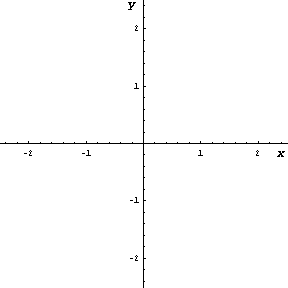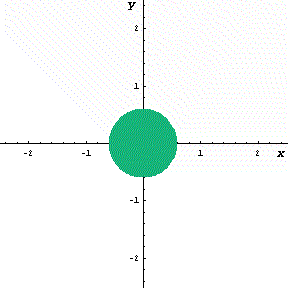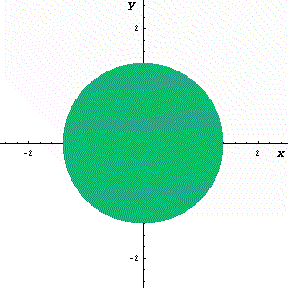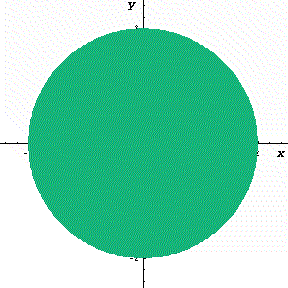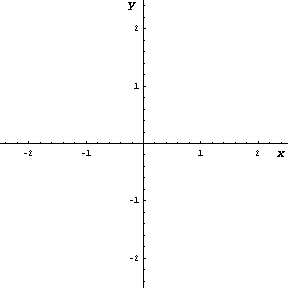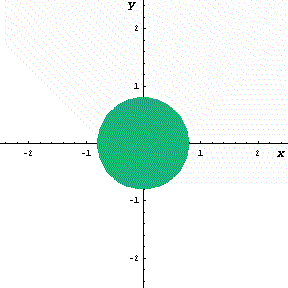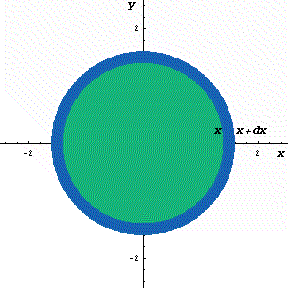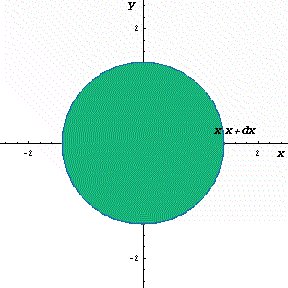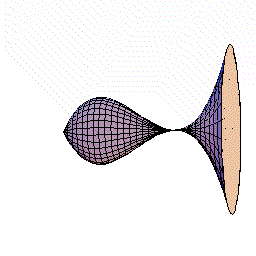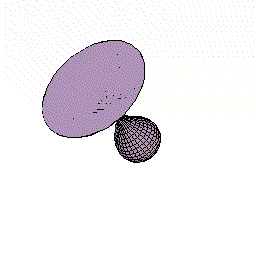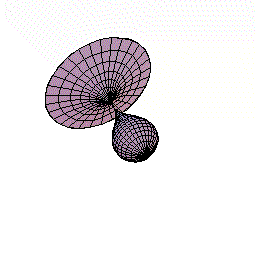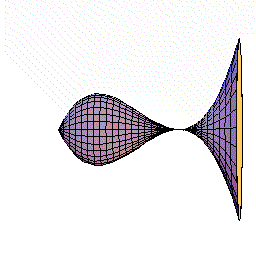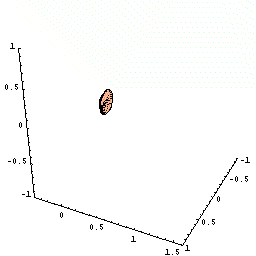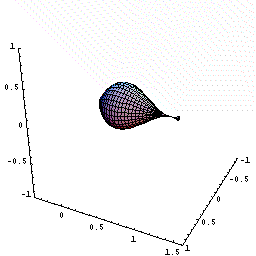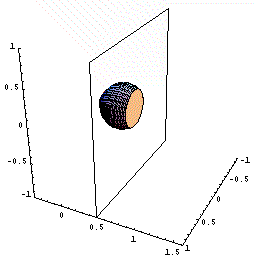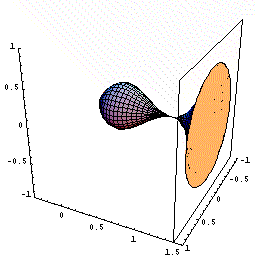6. 面積・体積の算出に見る「瞬間を捉える」というアイデアの凄さ
今まで見てきたように,「瞬間をどのように考えるか」という問題は,無限や極限を理解する問題でもあり,人類を千数百年間悩ましてきた大きな問題でありました。
この問題は17・18世紀にニュートン・ライプニッツ
等によって確立された「微分積分学」によって理解できるようになりました。これは人類にとっての大きな遺産です。これによって現代の科学技術が支えられているといっても過言ではありません。
さて「瞬間を捉える」というアイデアの凄さを,図形の面積や体積を求めることを通してみていきましょう。
まず直角二等辺三角形の面積を求めてみましょう。
三角形面積は底辺×高さ÷2ですからすぐに求まりますが,微分積分のアイデアを使うと次のようになります。
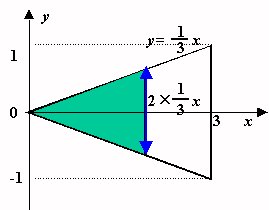
- 下図のように直角二等辺三角形を座標上に置く。
- 直角二等辺三角形の面積を,y=f(x)= xという関数と
x軸に挟まれた図形の面積と考える。
- この面積の瞬間の増加量dS/dxは f(x)=x である。
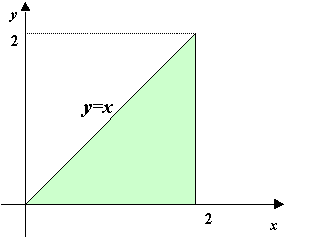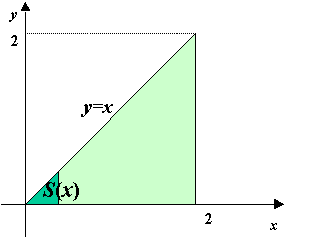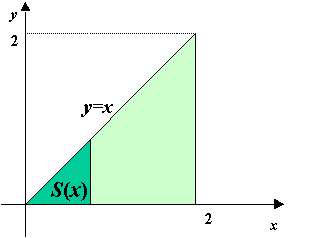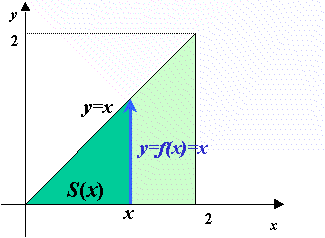
下図の動画は、x という瞬間に面積が関数値分だけ増加する
ようすを模式的に表したものである。
(ある瞬間における有限な増分の極限を青色で表示)
- 従ってS(x)はf(x)を積分すればよい。
- 求める面積はS(2)である。
- 直角二等辺三角形の面積の計算
|
|
では次に,円の面積を求めてみましょう。
考え方は終始一貫しています。すなわち下図のように、図形(円)がどんどん増加している状況を想像します。
- 下図のように円を座標上に置く。
- 円の面積が増加している状況を考える。
- この面積の瞬間の増加量 dS/dx は円周の長さの分である。
下図の動画は、x という瞬間に面積が円周分だけ増加するようすを
模式的に表したものである。
(ある瞬間における有限な増分の極限を青色で表示)
- 従ってS(x)は円周の長さ2πx を積分すればよい。
- 求める面積はS(2)である。
- 円の面積の計算
|
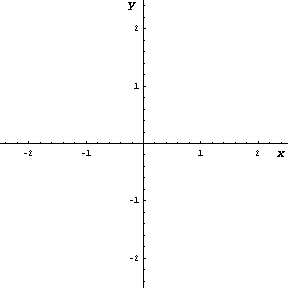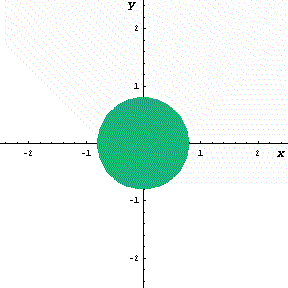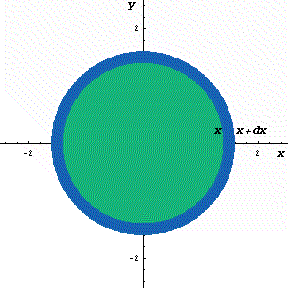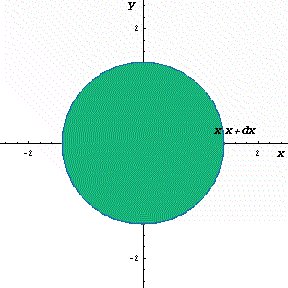
|
ここからは微分の考えを使って体積を求めていきましょう。
まず簡単な立体として,正四角錐を選びました。底辺の一辺が1,高さが3の正四角錐を考えます。
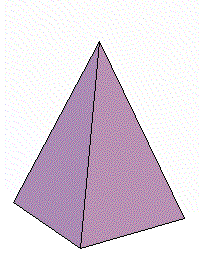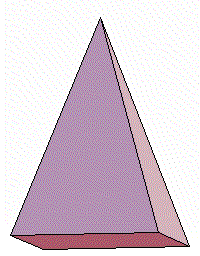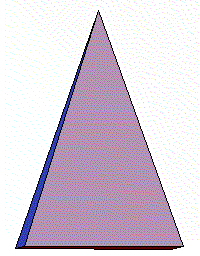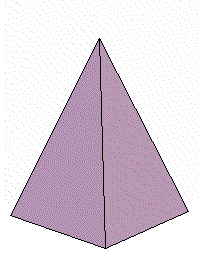
まず最初に考えなければならないことは,
- この立体はどのような立体が増加して,この形になったのか
- そのことを上手く記述するには,どのように座標をとればよいか
ということです。あなたはどう考えますか。
この立体の対称性を考慮すると,下図のように考えることが妥当でしょう。
すなわち、頂点を原点にして、底面に垂直な方向にx 軸をとり、x 軸方向に体積が増加している、と考えるわけです。
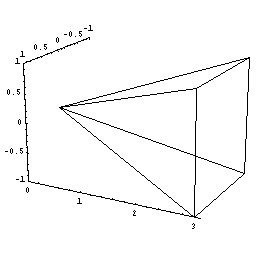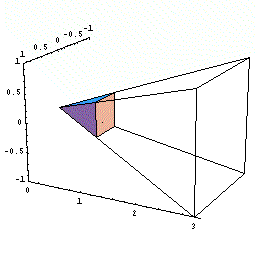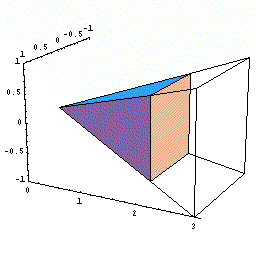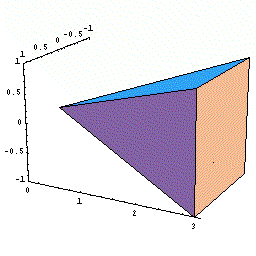
この様に座標を設定すると,この立体が瞬間に増加している増加分は,その底面積の分だけ増加している,と考えられます。
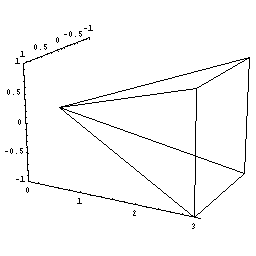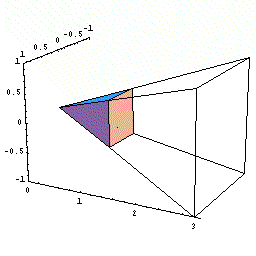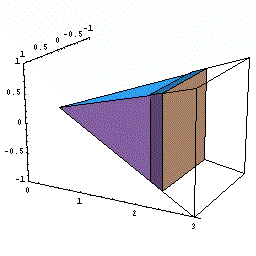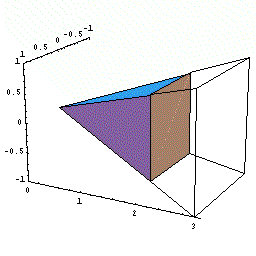
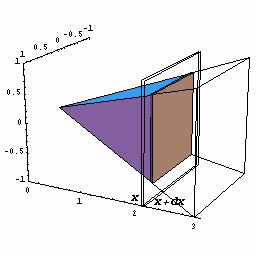
- 下図のように正四角錐を座標上に置く。
- 高さ0からxまでの正四角錐の体積をV(x)とする。
- xでのこの体積の瞬間の増加量dV/dxは,
正方形の底面積である。
下図の動画は、x という瞬間に体積が底面積分だけ増加するようすを
模式的に表したものである。
(ある瞬間における有限な増分の極限を茶色で表示)
- V(x)はその底面積を積分すればよい。
- 求める面積はV(3)である。
- 正四角錐の体積の計算
|
|
|
|
立体図形のもう一つの例として、球の体積を考えてみましょう。
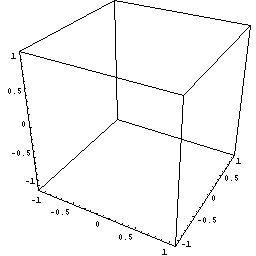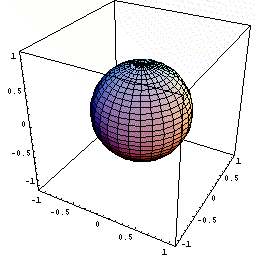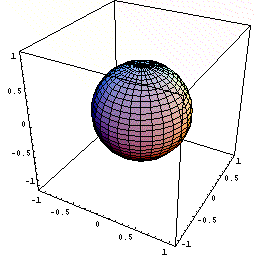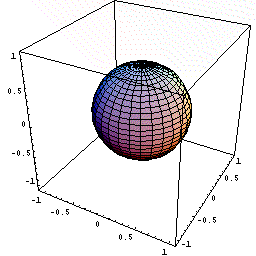
球は、最も対称性のよい図形ですので、下図のように、球の中心を原点にとり、半径方向にx 軸をとります。そして、半径の増加とともに体積がどのように増加するかを議論します。
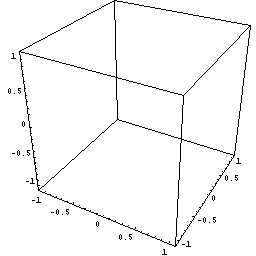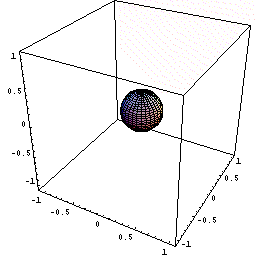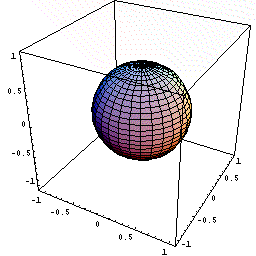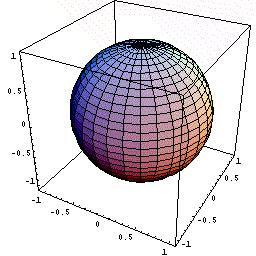
- 下図のように球の中心を原点に置く。
- 半径が0からxまでの球の体積をV(x)とする。
- xでのこの体積の瞬間の増加量dV/dxは,球の表面積である。
下図の動画は、x という瞬間に体積が表面積分だけ増加するようすを
模式的に暗示したものである。
(ある瞬間における有限な増分の極限を繰り返し表示しているため、鼓動のようにみえる)
- V(x)はその表面積を積分すればよい。
- 求める面積はV(1)である。
- 球の体積の計算
|
|
以上見てきたように,対称性の良い図形は,瞬間にどれだけ増加しているか議論がしやすいので,体積が求めやすいのです。
次に,やはり対称性のよい図形として回転体の体積を議論してみましょう。
下図のように,y=f(x)=2x(x−1)2=2x3ー4x2+2x(0≦x≦1.5)をx軸の周りに回転してできる図形を考えます。
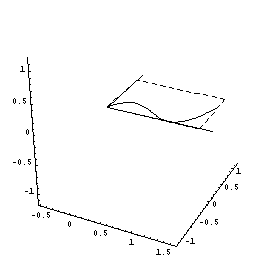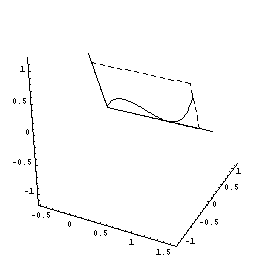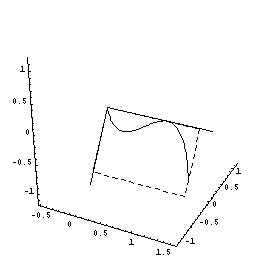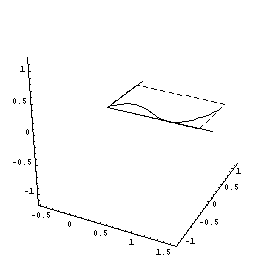
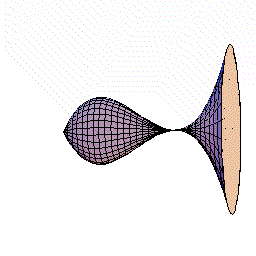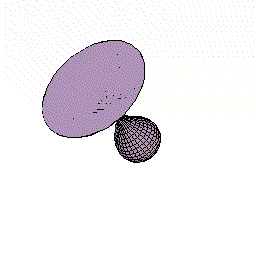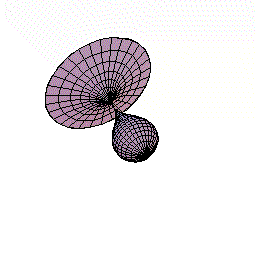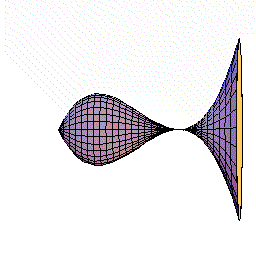
さてこの立体を,回転軸のxの位置で,軸に垂直に切断すると,0からxまでにできた立体V(x)が瞬間に増加する量は,その切断面の面積分であることがわるでしょう。
下図は、x が増加しているとき、ある瞬間にx 軸に垂直な面で切った切断面が円であることを示す動画です。
(切断面を、x=0.5で一瞬止める場合と止めない場合が交互に表現されています。)
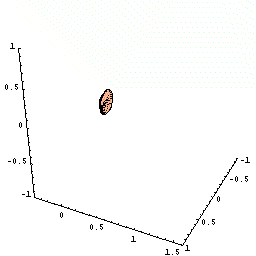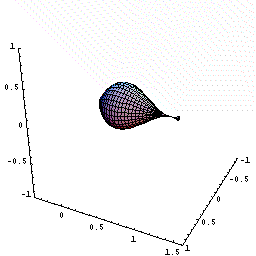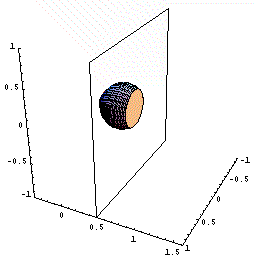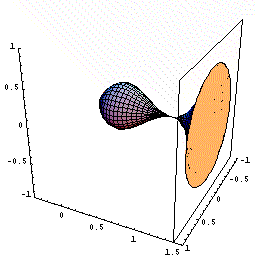
しかも,その切断面は半径がf(x)=2x(x−1)2の円ですね。
従って,dV/dx=π{f(x)}2であることも,もうわかりましたね。
- 下図のように回転体を座標上に置く。
- 回転軸の0からxまでの,この立体の体積をV(x)とする。
- xでのこの体積の瞬間の増加量dV/dxは,
断面の円の面積である。
- 曲線はy=f(x)=2x(x−1)2であるから,
断面積はπ{2x(x−1)2}2である。
- V(x)はその底面積を積分すればよい。
- 求める面積はV(1.5)である。
- 回転体の体積の計算
|

|
極限の話はいかがでしたか。
最初にお話した様に,人類が瞬間の出来事をうまく扱うようになるのに千数百年間かかりました。この考え方によって,その後の科学技術が飛躍的に発達しました。このような長い年月をかけて獲得した考え方の凄さに一端に触れてみて,いかがでしたか。
メニューに戻る