真東の方角と、真東に歩いていく方向の違い
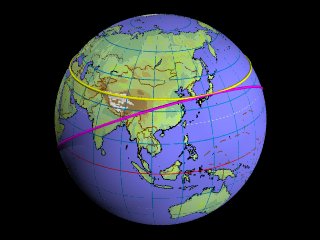
・黄色=常に真東に向いて歩いていく経路
上で述べた
「ある地点から真東の方角に位置する町には、真東に向かって歩いていっても着きません。」
という意味を詳細に調べてみましょう。
「真東の方角」とは、その地点にコンパスを置き、東を指し示す方角のことです。その方向へ球面に沿ってまっすぐ線を延ばしていくと、円を描いて地球を一周しますが、この円は、地球をその中心を通り真っ二つに割った円です。数学の用語で言うとこれは大円と呼ばれています。それは、球面上に描くことができる最大の円と言う意味を含めて名付けられています。地理学や航空などでは、地球上での大円のことを大圏コースとも呼んでいます。
一方、「常に真東に向かって歩く」とは、コンパスを携えて常にコンパスが指す東の向きに歩くことを意味します。つまり緯線に沿って歩くことになります。このように歩いていくと、円を描いて地球を一周しますが、この円は大円ではなく、小円(地球の中心を通らない円)になります。
真東の方角と、真東に歩いていく方向の違い
・黄色=常に真東に向いて歩いていく経路
|
上の地図だけではわかり難いかもしれませんので、コンピュータ・グラフィクス(CG) で仮想体験をしてみましょう。
岐阜市から、真東の方角に行くと
|
岐阜市から、常に真東の方角に歩くと
|
いかがでしたか。
「岐阜市から、真東の方角に行く」とは、岐阜市と地球の中心を通り、岐阜市における緯線に接する大円に沿って進むことを意味します。この場合、緯線から次第に離れるとともに、歩いている向きは東から南よりになってきます。この様子は、コンパスを見ていれば分かります。
一方
「岐阜市から、常に真東の方角に歩く」とは、岐阜市における緯線に接する大円に沿って進むことを意味します。この場合、コンパスを携えて、真東の方角へ少しずつ左に向きを変えながら進むことになります。
「真東に行く」ことをまとめると、次のようになります。
|
しかし、「真東の方角に行く」という言い方に対しては、
|
さて次に、もうひとつ明確にしておくこととして、
「球面上で、まっすぐとは、あるいは直線とはどういうことか」
ということです。
平面上での直線は、明らかでしょう。
「直線とは、2点を結ぶ最短コースを無限の彼方まで伸ばした、太さのない棒のようなもの」 です。
「・・・のようなもの」という言い方が曖昧に感じるかもしれませんね。
実は平面幾何学では、直線という概念は、多くの人が誤解をせずに頭に描けうるものであり、他の概念から二次的に定義されるものではない、としています。
このような概念を、数学では未定義概念と言い、定義をする以前に存在しているものと見なしています。従って、直線の定義を記述しようとしても当たり前過ぎて、かえって記述し難いことなのです。
このような未定義概念として、「点」「直線」「平面」があり、これらをもとに、他の概念が定義されていきます。
例えば、
などのように、新たな概念が定義され、生まれていきます。
では、球面上の幾何学における「直線」とは、何でしょうか。
「球面上の直線とは、球面上の2点を結ぶ最短コースであり、その2点と球の中心を通る平面で切ったときの球面上の切り口のこと」です。これは、2点を通って球面上に描くことができる最大の円という意味を込めて、大円と呼んでいます。ですから球面上の直線は、平面上の直線とは異なり、円なのです。
大円が2点を通る最短コースであることが納得できない人のために
従って、
地球上の2点AB間を「まっすぐ最短に」結ぶためには、2点A,Bを通る大円を描けばよい、これが2点を結ぶ「球面上の直線」ということ
です。
以上より、地球上の2点を結ぶ直線(最短コース)と2点の方角について整理すると、
ということになります。
実例を観てみましょう。
岐阜市から、アメリカ西海岸付近の同緯度の地点
|
上の図のように、岐阜市からアメリカ西海岸の同緯度の地点(ロサンジェルス付近)までの最短コースは、緯線よりもかなり北寄りのコースとなっていることに注意してください。
さて最後に、
再度念のために、「真東へまっすぐ歩いていくと、どこに行くか」という問いの解答を整理しておきましょう。
要するに、 常に真東に向かって、まっすぐ歩くことは不可能ということです。
以上のように、球面幾何学は、平面幾何学とは趣の異なる展開になってきました。
