歴史を振り返ると，大昔から音階らしきものはあったのですが，古代ギリシャ，ローマ，中世を経て，洗練されたものになりました。ここに展示する 純正調の音階は，ピタゴラスとその学派によってその基本が作られましたが，その美しさと合理性は驚くべきものです。十分楽しんでください。

まず，音とは何でしょうか。言うまでもなくそれは空気の濃い薄い（粗密）という特殊な状態のことです。これが伝わって耳に入り音として聞こえるわけです。 音の原理が最も目で見やすく理解できる道具は，弦の振動でしょう。弦を弾くと節と腹ができて振動する様子がみえます。この振動が空気を粗密にして 音となりますので，音を直接見ているといってもよいでしょう。

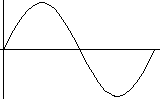
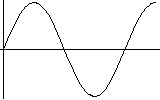
さて、まず基準となる「音を観て」みましょう。

下記に、その音を発する弦、その音を数学的に表現したグラフ（１周期分）、実際に発する音（聞くことが可能です）を展示します。



さて弦の長さを変えると音の高さが変わります。短くすると高くなり，長くすると低くなります。これは弦の振動が短くすると速くなり，長くすると 遅くなるからです。専門用語で言うと振動数が変わるといいます。ではどのように長さを変えると，あの音階ができるのかみていきましょう。

ある長さの弦から始めて，長さを短くしていくと，ちょうど長さが半分になったところで，元の音（主音）と高さは違うが同じような音になります。この音を オクターブ上の音といいます。このふたつの音が同じよな性質に聞こえることが面白いですね。元の音がドならばこの音もド’（オクターブ上と言う意味で ’をつけましょう） というわけです。



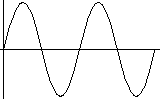
このとき弦の長さ（波長）が半分になれば振動の回数（振動数）は２倍になるという物理的な性質にも注意してください。 弦の長さをさらに半分，元の長さの１／４にするとどうなるでしょうか。



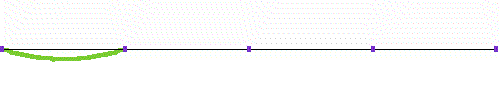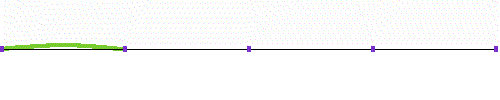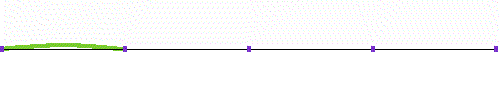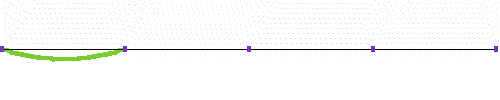
この様に，弦の長さを１／２，１／４，１／８，１／１６，･･･，振動数を２，４，８，１６，･･･としていくと，音の高さはオクターブずつ上がっていきます。 逆に弦の長さを２，４，８，･･･倍，振動数を１／２，１／４，１／８，･･･としていくと，音の高さはオクターブずつ下がっていきます。

さて次に，弦の長さを１／３，１／５などにしたらどんな音になるでしょうか。まず弦の長さを１／３振動数を３倍にした音をきいてみましょう。



ずいぶん高い音ですね。これを２倍してオクターブ下げてみましょう。弦の長さは１／３×２＝２／３となり，１と１／２の間に入ってきます。これはどんな音なのか 聞いてみます。



そうです，いわゆるソの音です。

同様に弦の長さが１／５の音を見てみましょう。この音もそのままでは高すぎますから，１と１／２の間に入るように２オクターブ下げて１／５×２×２＝４／５にして，音を 聞いてみますと，ミの音になります。



これでド，ミ，ソ，ド’ができました。 以上を整理すると，最初の音をドとすると，ド，ミ，ソ，ド’は，弦の長さでいうと，１，４／５，２／３，１／２，振動数でいうと１，５／４，３／２，２の比率になっているわけです。 ここで面白いことがみえてきます。それは，音の高さの違い（音程）は「差」ではなく「比」を感じているのだ，と言うことですね。ド，ミ，ソ，ドの弦の長さの 比率は，３０：２４：２０：１５であり，振動数の比は，４：５：６：８ということになります。

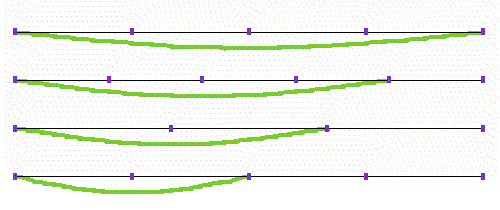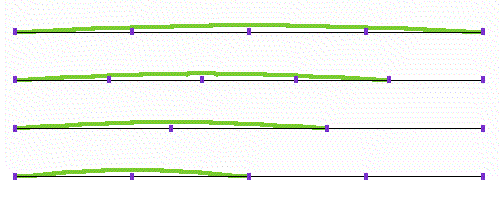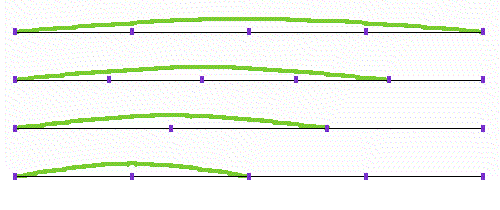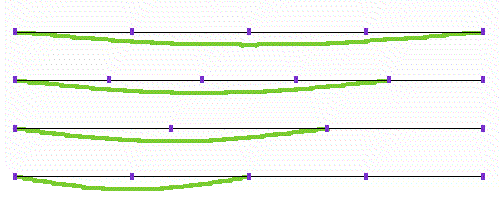
さて不完全ですがド，ミ，ソ，ド’という音階の骨組みができましたので，ここでその音の性格づけをしましょう。

音階は階段に似ています。ドが１階でド’が２階とみなすのも自然でしょう。１階から一足飛びに２階に上がるのは大変ですので途中の休憩地点が必要です。この音階をよく聞いてみると，ソがその役目をしています。ちょうど階段の踊り場のようなものです。 ドの位置にいるとソに行って一服したくなり，ソの位置にいるとドやド’に行って安心したくなる気がします。ソの音の存在はドやド’の存在をさらにはっきり意識させてくれます。そういう意味で，ソはド（主音）の属音（ドミナント）と呼んでいます。「メロディーとはドミナントへの弾道である」 と言ったのはストラビンスキーだったでしょうか。

ドとソの関係とソとド’の関係は微妙に違います。振動数でいうと，前者は３／２の関係であり，後者は４／３の関係ですから， ソはド’寄りにあります。決してドとド’の真ん中ではありません。ドからソへの跳躍はソからド’への跳躍よりも，より自然です。それは振動数の比が２：３という極めて 単純な比になっているからに他なりません。ソとド’では３：４であり，これよりも単純であり，ドとド’の１：２よりは複雑になっています。このドとソの２：３の跳躍関係（完全５度の跳躍）は， 残りのレ，ファ，ラ，シを作り出す大切な感覚になります。

さっそく，レ，ファ，ラ，シを作りましょう。まず議論を分かり易くするために弦の長さだけで見ていきます。まずミの完全５度上の音を作ると４／５×２／３＝８／１５となりソとド’の間の音になります。 これをシと呼んでいるわけです。

次に，ソの完全５度上の音を作ると２／３×２／３＝４／９となりドからド’の間からはみ出しますのでさらにオクターブ下げて４／９×１／２＝８／９とするとレができます。 次にド’から完全５度下がる（ソからドへ戻る比率）音を作ります。それは１／２×３／２＝３／４となり，ミとソの間の音になり，これがファです。

次に，ミを作ったときに使った１／５をオクターブ下げて２／５とし，それを完全５度下げると，２／５×３／２＝３／５となり，ソとド’の間になり，これがラです。

これでやっとドレミファソラシドができました。ここまで作るのは大変でしたが，歴史的にみるとこれらがこの形に落ち着くのに約１０００年はかかっていますから，それに 比べるとあっという間でしたね。

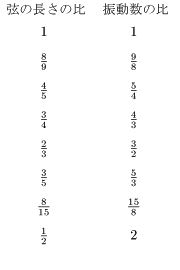
何度も言うように音程は比率の感覚ですから，ドレミファソラシドは等間隔に並んでいるのではありません。この音階の中にある比率を整理すると， ド：レ：ミ：ファ＝ソ：ラ：シ：ド’ ド：ソ＝ミ：シ＝ファ：ド’ となっています。つまり，ドレミファとソラシドは，調は違いますがどちらもドレミファと聞こえますし，ミシ，ファド’の跳躍も調は違いますがドソの音程と同じ様に聞こえるわけです。 単純な比率を持つ音どうしは，振動のエネルギーを受け渡しやすいという性質（共振）を持っていますので，それらの音は非常によく響き合います。 この音階はそのような単純な整数比の音程からできていますので，自然に響き合う音階です。これを純正調の音階といいます。純正調音階は，もともと自然法則に基づいて響き合う 音を連ねたものですから，神が作った音階と言えるのではないでしょうか。

しかし、この音階の決定的な欠陥は転調ができない点にあります。例えばニ長調では、レとラの比率は(３／５)÷(８／９)＝２７／４０であり、完全５度の音程２／３にはならないので、 ニ長調の音階は不自然で聞きづらいものとなってしまいます。 この欠陥は，音楽が発達し複雑になってくると，その発達を阻害するようになってきました。そこでこの困難を克服するために開発された音階が平均律による音階です。 まるで数学の世界において，自然数だけでは議論が十分にできなくなり，数を整数，分数，無理数，そして虚数と拡張していった歴史に似ています。 次の節で，平均律の音階の仕組みを見ていきましょう。