- 【音楽と数学のいろいろ】 目次
- 1.「神が作った?音階」=純正調音階について
- 2.「人間が作った音階」=平均律音階について
- 3.和音の流れについて
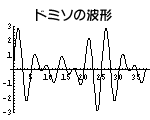
- 4.音色について
- 2.「人間が作った音階」=平均律音階について
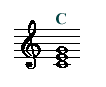
|
音楽は,自然を対象とすることもありますが,やはり,喜び,悲しみ,憧れ,勇気,落胆,・・・などの人間の心の有様を対象にしていることが多いですね。
一方数学の対象は,自然現象や社会現象などが中心です。数学も人間の心の有様を対象としたいのですが,扱い難いことも事実です。 音楽は,これらの対象を,人間の感性を通してどのように見えるかを表現しようとしますし,数学は、これらの対象を,人間の知性を通してどのように見えるかを表現しようとします。この様に音楽と数学は,大きく趣を異にしていることは事実です。 しかし,「どのように見えるかを表現しようとする」という点で共通するのではないでしょうか。音楽は対象を音という手段で「象徴的に表現」 をし,理解しようとします。数学は対象を記号という手段で「抽象的に表現」をし,理解しようとします。一般に,対象を何らかの手段で表現をするときには 対象を「モデル化」する必要があります。 「モデル化」の例として,音楽において,「喜び」を表そうとしましょう。「喜び」は音楽そのものではありませんから,「喜び」とは何かを 分析し,音楽という形態に乗せやすいように加工して,その「喜び」に類比した音の連なりに変換して表現します。これが音楽における「モデル化」です。 また、数学において,例えば「三角形」(ここで言う「三角形」は,三角形状をした具体的な物を想定しています)を表そうとしましょう。「三角形」そのものは数学ではありませんから,「三角形」とは何かを分析し,数学の記号に乗せやすいように 加工して,その「三角形」に類比した記号の列に変換して表現します。これが数学における「モデル化」です。 音楽と数学の「モデル化」の手法はそれぞれ異なりますが,対象を,それとは異質のもの(音あるいは記号)によって本質に近いものを表現する営みは共通しています。 つまり,言い換えると,どちらも人間が何かを認識しようとするときの言語である,ということです。
さらにもうひとつ大切な共通点があります。それは「モデル化」における「美学」です。 人間の歴史を振り返ると,古代においては,数学も物理学も音楽も美術も,そして学問全体が一体化していました。特にピタゴラス(とその学派)は,宇宙を 数と音楽で表現しようとしたことは有名ですし,レオナルド・ダ・ヴィンチもそれらを統合した業績を残しています(このことは彼自身の天才性に負うわけですが, その時代的な背景も無視できない)。音楽を英語で言うとmusicですが,そのmuseという語幹は,ギリシャ神話に出てくる文芸と学術を司る神を連想しますし,沈思する という意味もあります。一方,数学を英語で言うとmathematicsですが,語源であるギリシャ語のmatheinはよく考えるという意味です。 どちらも元々は,ものごとをよくみる,という共通した営みを表していたようです。時代が進むに連れてそれぞれの学問が分化をして発達し,現代に至っているわけですが, その根本精神はそれほど分化していないのではないでしょうか。 |
前置きが長くなりましたが,ここでは数学から見た音楽の話題をいくつか展示してあります。ご鑑賞ください。
|

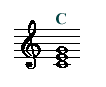
|
| 「和音の流れについて」より |