「風」という対象物には、風の強さのみならず、吹いてくる向きも欠かせな
い要素です。
また、「風」は温度や湿度などの属性も持っていますが、気象
学上では、例えば「南南西の風、風力3」というように、大きさと向きを属
性として持っている量であるようです。このような量をベクトル(vector)
あるいはベクトル量と呼びます。
(右の写真は高知大学・東京大学・気象庁 提供)


|
夏になると涼やかな南風、冬になると肌を切る北風・・・というように、 「風」という対象物には、風の強さのみならず、吹いてくる向きも欠かせな い要素です。 また、「風」は温度や湿度などの属性も持っていますが、気象 (右の写真は高知大学・東京大学・気象庁 提供) |

|

|
| 夏の風 | 冬の風 |
ベクトル量の別の例としてよく取り上げられるのは「力」です。
「力」も大きさだけではなく、引っ張られているのか、押されているのか、上向きなのか、下向きなのか、という向きを明言しないと、「力」を表現し尽くしたことになりません。
このようなベクトル量に対して、大きさだけで言い尽くせる量をスカラー量(scalar)といいます。例えば、物の長さ、面積、体積、質量などがスカラー量です。
ところで余談ですが、
|
私たちは、質量、重量、重さ、物体に働く重力という量については、その違いをあまり意識しておらず、その使い分けも曖昧ですね。 ベクトルかスカラーかは微妙なところです。実は正確に言うと、
たとえば、質量10キログラム(kg)の物体の重量または重さは、10×g≒98ニュートン(Nまたはkg・m/sec2)です。 これを10キログラム重(kilogram force)とも言いますので、いつの間にか日常的には、単に10キログラムと言っています。 この物体に働く重力は、鉛直下向きに約98ニュートン(または10キログラム重)である、と言います。 この物体を月面へ持っていくと、質量は10キログラムと変わりませんが、重量は約1/6倍となり、小さく(軽く)なります。 ここで一つ問題を出しましょう。
|
さて、ベクトルの表現方法をみていきましょう。
|
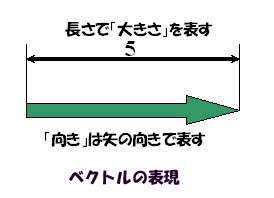
大きさと向きを持つ量として定義されたベクトル
の表現方法は、視覚的にわかりやすい 矢線で表されます。 また記号としては 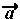 , ,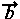 ,・・・ のように ,・・・ のように
アルファベットの上に矢印を付けて表します。 |
|
|
このように、大きさと向きを強調した表現を、ここでは、ベクトルの「幾何学的表現」と呼ぶことにしましょう。
このように定義されたベクトルの表現方法は、その要素を数値で表して並べ、それら全体をひとつのセットとして、括弧( )を付けて表します。
例えば、(2,3)、(2,3,4,5)のようになります。記号としては ,
, ,・・・のようにアルファベットの上に矢印を付けて表すことは、上記の「幾何学的表現」の場合と同じです。
,・・・のようにアルファベットの上に矢印を付けて表すことは、上記の「幾何学的表現」の場合と同じです。
このように、複数の数値のセットとしての表現を、ここでは、ベクトルの「代数学的表現」と呼ぶことにしましょう。
|
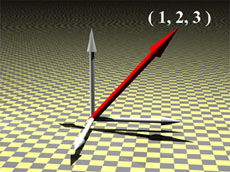
この表現方法は、座標上の点と同じ表現であることに気がつくでしょう。
実はその通りであり、ベクトル(1,2)は、座標平面上の点(1,2)と同じであると考えて差し支えありません。 すなわち、ベクトルの始点を原点に置いたときの終点の座標であると認識すればよいわけです。 このように考えると、
|
|
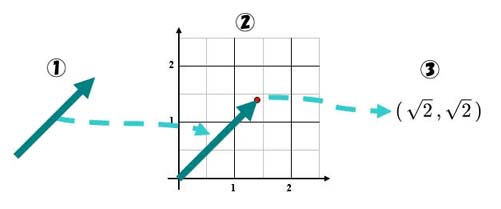
それではここで、正面玄関(幾何学的表現)から入って、裏玄関(代数学的表現)までの議論の全貌を見ていきましょう。
まず、南西の風、風力2のベクトルを考えます。
|
|
このように、座標平面を利用して、幾何学的表現と代数学的表現が一意に決まります(一通りに表現でき、しかも行ったり来たりして復元できる)ので、同じもの(同値)である、ということになります。
今度は別の例で、代数学的表現から入って幾何学的表現へもっていきましょう。
|
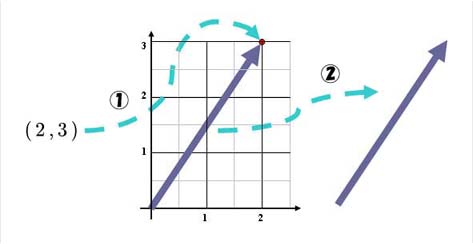
|
以上、
ベクトルの幾何学的定義と代数学的定義は、
ベクトルの始点を原点にもってくることにより、大きさ・向きと、終点の座標の関係が
明確になり、同一視できる、ということです。
このことを、「ベクトルの2通りの定義による表現方法の違い体感シミュレータ」で味わってみてください。
さて最後に、また余談になりますが、
|
ところで、学校の成績については、例えば期末テストの点数が、(国語、数学、英語)=(85,65,90)であったとき、
|
