2つの風が重なり合う、2つの力が合成されるなど、2つのベクトルを加えるという感覚は、直感的にわかりやすいものです。
まず幾何学的表現のベクトルについて、次のような2つのベクトルの和を考えましょう。

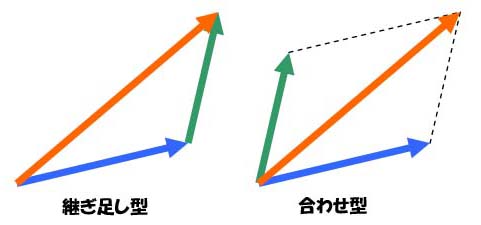
単純に「和」といっても、次のような2通りの考え方ができます。
|
右図の左の考え方は、例えば、
「岐阜から名古屋へ行き、さらに名古屋から東京へ行くと、 岐阜から東京へ行ったことになる」という感覚であり、 「継ぎ足し型」と呼ぶことにしましょう。
|
|
次に代数学的表現のベクトルの和はどうなるでしょうか。
|
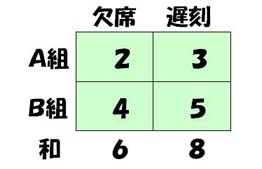
例えば、学級の出欠状況(欠席、遅刻)を調べたところ、
A組は(2,3)であり、 B組は(4,5)であったとすると、 合わせて (2+4,3+5)=(6,8)を和とすることは、 自然に納得できると思います。
| 
|
さて、上記のように2つの方法で表現されたベクトルの和が、同一のものであることを確認しましょう。この場合、「継ぎ足し型」による説明がわかりやすいです。
|
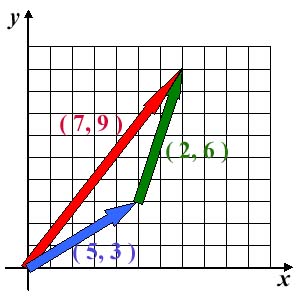
右図のような青ベクトルと緑ベクトルの和を考えると、
継ぎ足し型で生成した和の赤ベクトルが、 要素どうしの和になっていることはすぐに分かるでしょう。 |
|
「1 ベクトルとは何か(定義について)」で見てきたように、日常的な量の多くがベクトル量であったことから、ベクトルの和も日常的な現象で大いに活躍します。ここではその事例として「力」に関するものを3つ紹介します。
| |
| |
|
|
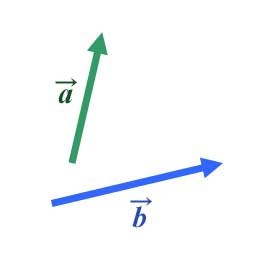
さて、下図の2つのベクトル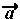 ,
,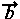 について、「差」
について、「差」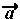 -
-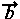 を考えていきましょう。
を考えていきましょう。
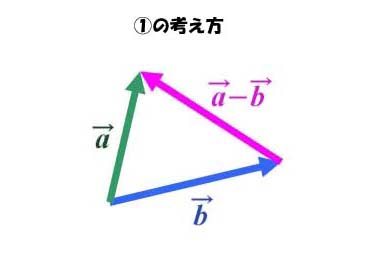
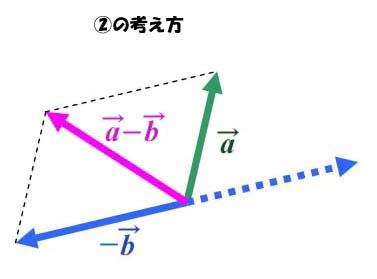
ベクトルの「差」についても、スカラーと同様に、2通りの考え方ができます。
|
|
|
ベクトルの和差の最後として、「ベクトル演算シミュレータ(和差編)」で遊んでみましょう。
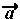 を2つ加える、すなわち
を2つ加える、すなわち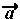 +
+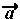 は、幾何学的表現で言うと、大きさが2倍となり、向きは同じベクトルです。ところで、普通の数(スカラー量)の a + a は 2a と表すように、
は、幾何学的表現で言うと、大きさが2倍となり、向きは同じベクトルです。ところで、普通の数(スカラー量)の a + a は 2a と表すように、
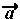 +
+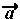 ベクトルも 2
ベクトルも 2 とすると分かり易いですね。
とすると分かり易いですね。
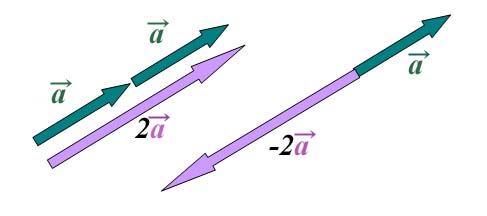
というわけで、
k倍の は、向きは同じで大きさをk倍したもの、とします。ただし、kが負のときは
向きを反対にすることとしましょう。こうすると、「2-2 ベクトルの差」でみたように、
は、向きは同じで大きさをk倍したもの、とします。ただし、kが負のときは
向きを反対にすることとしましょう。こうすると、「2-2 ベクトルの差」でみたように、 の逆ベクトル-
の逆ベクトル-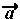 が-1倍の
が-1倍の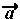 であると解釈すればよく、これも都合がよいですね。
であると解釈すればよく、これも都合がよいですね。
また、kは整数でなくてもよく、例えばk=2.5であれば、大きさが2.5倍となっているベクトルを考えればよいことになります。
このような過程をみていくと、「数学はずいぶんご都合主義!?だな」と思うことでしょう。
実は、数学は考え方や記号を拡張していくとき、法則の終始一貫性や整合性を大切にするからです。
つまり、見かけ上異なって見えるいくつかの対象物も、できる限り単純な法則で普遍的に統一的に議論できるようにしたい。そのためには、見かけ上異なるもの同じものである見なそう、という考え方に立ちます。これが数学的な精神であり美学であると、考えます。
