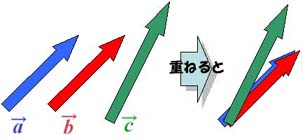
右図のように、３つのベクトルがあります。 青と赤は、平行移動させれば完全に重なりますので、全く同じベクトルです。 当然、代数学的表現をしても同じです。 一方、青と緑は、平行移動しても重なりませんので、全く違うベクトルです。 緑は、幾何学的な言い方をすれば、青の向きを変え伸び縮みさせる操作をしたものであり、 代数学的な言い方をすれば、終点の座標を動かしたもの、と言うこともできます。

「ベクトルを動かす」ということは、平行移動させるという意味（青→赤）と、異なるベクトルを作り出すという意味（青→緑）があります。ここでは後者の意味で、「ベクトルを動かして」みましょう。

　ベクトルの代数学的表現は、始点を原点にとることにすれば、終点の座標と同じであったので、べクトルを動かすことは、その終点の座標を動かすことと同じです。

「ベクトルや点が刻々と動く」とは、点の座標（ ｘ，ｙ ）が、（ ｔ の関数，ｔ の関数 ）のように、時間 ｔ の関数で表現されているということです。
たとえば、

ｔ を時間と考えて、 　　（ｘ，ｙ）＝（２ｔ−３，３ｔ＋１） とすると、 　　ｔ＝０ のとき、（ ｘ，ｙ ）＝（−３，１ ） 　　ｔ＝１ のとき、（ ｘ，ｙ ）＝（−１，４ ） 　　ｔ＝２ のとき、（ ｘ，ｙ ）＝（　１，７ ） また、時間をさかのぼって負の値も考えると、 　　ｔ＝−２ のとき、（ ｘ，ｙ ）＝（−７，−５ ） となります。 さらに細かく ｔ を変化させるとき、 例えば、０．２刻みで時間をとると、 右図の表のようになります。 これをグラフ上に描くと、 時間 ｔ とともに点（ ｘ，ｙ ）が動く様子が 分かります。 この点が描いた図形を数学では 「軌跡」と呼びます。 また、ｔ のことを媒介変数と呼びます。 　　この言葉の由来は、 　　ｘ 座標と ｙ 座標が、変数 ｔ を媒介にして 　　間接的に結びつけられていることから 　　来ています。また、これを parameter と 　　も言います。 　　　　ｘ＝２ｔ−３，ｙ＝３ｔ＋１ 　　の２つの式から、 　　ｔ を消去すれば、 　　　　３ｘー２ｙ＋１１＝０ 　　となり、 　　これは軌跡（この場合は直線）を表す 　　方程式が出来上がります。

４−２　ベクトルを動かして、遊んでみよう

ここでは、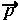＝（ ｘ，ｙ ）＝（ ｔ の関数，ｔ の関数 ）が、時間 ｔ （媒介変数）とともに動く様子を、３つのタイプの「『動くベクトル』シミュレータ」で観察してみよう。

�@ ｔ の１次関数で 　　　表現されるタイプ 　◆＝（ｘ，ｙ） 　　＝（ ａｔ＋ｃ，ｂｔ＋ｄ ） 　　で表現されている。 　◆ａ，ｂ，ｃ，ｄ は、 　　-10 から 10 の間で、 　　0.1 刻みで指定できる。 　　（各スライダで設定） 　◆ｔ は、-10 から 10 の間で、 　　0.1 刻みで動かすことが 　　できるほか、指定した最小 　　値と最大値の間で、0.1 　　刻みで、自動的に動かすこ 　　とができる。（traceボタン） 　　動かすスピードも調整可能 　　である。（speed スライダ） 　【観察の観点】 　　※（ａ，ｂ）は、どんな 　　　意味のベクトルか？ 　　※（ｃ，ｄ）は、どんな 　　　意味のベクトルか？ 　　※の終点は、 　　どんな図形を描くか？ 　　また、その図形の方程 　　式はどうなるか？

�A ｔ の２次関数で 　　　表現されるタイプ 　◆＝（ ｘ ，ｙ ） 　　＝( at2+ct+e, bt2+dt+f ) 　　で表現されている。 　◆ａ，ｂ，ｃ，ｄ は、 　　-10 から 10 の間で、 　　0.1 刻みで指定できる。 　　（各スライダで設定） 　◆ｔ は、-10 から 10 の間で、 　　0.1 刻みで動かすことが 　　できるほか、指定した最小 　　値と最大値の間で、0.1 　　刻みで、自動的に動かすこ 　　とができる。（traceボタン） 　　動かすスピードも調整可能 　　である。（speed スライダ） 　【観察の観点】 　※（ａ，ｂ）はどんな 　　意味のベクトルか？ 　※の終点は、 　　どんな図形を描くか？ 　　また、どうしてそのよ 　　うになるのか？

�B ｔ の三角関数で 　　　表現されるタイプ　　 　◆＝（ ｘ ， ｙ ） 　　＝( a cost+c, bsint+d ) 　　で表現されている。 　　2×2 行列とベクトルの積 　　で表している。 　◆ａ，ｂ，ｃ，ｄ は、 　　-10 から 10 の間で、 　　0.1 刻みで指定できる。 　　（各スライダで設定） 　◆ｔ は、-10 から 10 の間で、 　　0.1 刻みで動かすことが 　　できるほか、指定した最小 　　値と最大値の間で、0.1 　　刻みで、自動的に動かすこ 　　とができる。（traceボタン） 　　動かすスピードも調整可能 　　である。（speed スライダ） 　【観察の観点】 　※（ａ，ｂ）はどんな 　　意味のベクトルか？ 　※（ｃ，ｄ）はどんな 　　意味のベクトルか？ 　※の終点は、 　　どんな図形を描くか？ 　　また、その図形の方程 　　式はどうなるか？