
『ゼノンの逆説』 |
|
これらゼノンの逆説(パラドックス)は明らかにおかしいですが,どこがおかしいのかを明確に 答えられるようになったのは,何と18世紀ごろになって微分積分学が芽生え始めてからです。
さて,この逆説の中にあるように,「永遠に」とか「瞬間」といった概念を正しく理解するには,無限の概念をはっきりさせなければなりません。そこで,ここでは無限についてのいくつかの話題を展示しました。
ごゆっくりご鑑賞下さい。
|
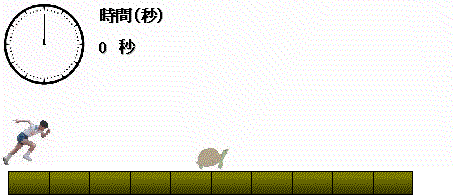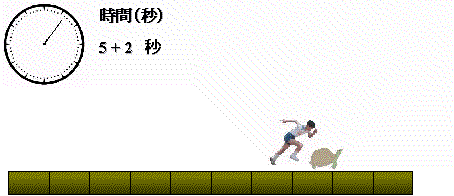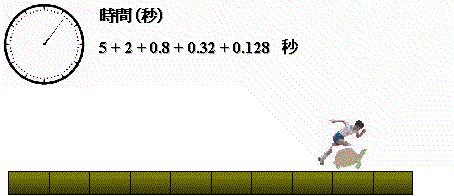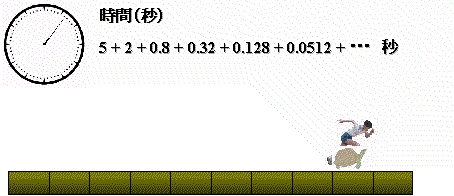
この様に,アキレスが亀の位置まで行くのにかかる時間は,
5+2+4/5+16/32+・・・
ですから,
加える時間は小さくなっていくものの,無限に加えていくので,その時間はどこまででも大きくなり,いつまで経っても追い越せない
となるわけです。どこか変ですね。
ここまでくると問題の核心が見えてきました。つまり,
5+2+4/5+16/32+・・・が有限か無限か,
ということを議論すればよいわけです。
ところで,この無限和はどのようになっていくのでしょうか。ここに29項までの和を順次計算したものを下に示します。
この無限和を29項まで計算すると
この様に,この無限和はある値を超えません。つまり有限な値に収束します。
ここでちょっと数学を思い出すと,
無限級数について
ですから,アキレスが亀の位置まで行くのにかかる時間は
25/3=8.333・・・秒
であり,決して「いつまで経っても」追いつけないのではありません。 つまり,この無限和は追いつくまでの時間を計算していることになるわけです。
従ってゼノンの逆説を正しく言うと,
「・・・この状況はいつまででも続くのではなく,有限の時間までであり,それはアキレスが亀に追いつくまでである。」
というべきです。
「数字を無限に加えていっても無限に大きくなるとは限らない」ということを理解することが大変難しいことだった,ということです。
どんなに低くなっても跳ね返ることは確かですから,このボールは永遠に止まらない
という主張はどうでしょうか。もちろん摩擦はないものとして考えます。

ちょっと物理の復習をしましょう。
物理の復習
今の「物理の復習」で出てきた式の中の
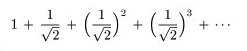
が無限等比級数であり,-1<公比<1を満たしますから,この和は有限な値です。 これから分かるように,床に落ちるまでの時間の累積は有限な値になりますから,その値になったとき静止するということです。従って
いつまでも弾むわけではありません。
0.3+0.03+0.003+0.0003+0.00003+・・・
でしょう。
この数字は,0.3333333・・・ですから,明らかに(本当に明らかでしょうか?)1/3であり,有限な値です。しかも
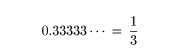
と書いても違和感はないようです。しかし,
0.99999・・・=1
については,多くの人が違和感を感じるようです。
0.9999・・・の方がほんの少し小さいような気がする人が多いのではないでしょうか。これがぴったり1であることを納得するには次のような方法が
あります。
これで納得
方法1と2は本質的には大きな違いがありませんが,方法2の方が数字の自己相似形(フラクタルのいろいろを参照)を意識した考え方です。
この様に0.9999・・・はぴったり1なのです。前者の方がやや小さいと感じるのはまさに「気のせい」です。
0.3333・・・と1/3において
前者がやや小さいと感じないのは,1/3のわり算を筆算で体験したことが利いているのだと思います。
0.3333・・・=1/3は納得しても,
0.9999・・・=1が納得できないのはやや「えこひいき」なのかもしれません。0.3333・・・の方も1/3にはやや足りないと感じる人は
極限値の意味を理解すれば腑に落ちるでしょう。それでも納得できない人は次を見て下さい。
下の計算は1÷1を積み算で計算しています。ただし,最初に1を立てるとそれで終わってしまいますので,あえて0を立てて計算します。
1÷1の積算
どうでしょうか,これで0.9999・・・=1が納得できましたか。
さて,今まで無限に数字を加えていっても有限である数を見てきました。これらの特徴は加えていく数字がだんだんに小さくなっていくような ものでした。加えていく数字がだんだんに大きくなっていくものは当然無限になります。たとえば,
1+2+3+4+5+・・・は明らかに無限(∞)
です。
ところで,加えていく数字がだんだん小さくなっていくような数字が有限であるか,無限であるか,の判断は,大変厄介であり微妙な問題です。
次の数字は有限でしょうか,無限でしょうか。
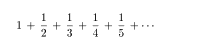
下の式は,30,000項まで加えていった和を順次表示しています。
これからわかることは,
「この和は少しずつ大きくなっていくが,その速さはとても遅い。ひょっとしたら有限の値になるかもしれないし,無限かもしれない。」
ということでしょう。実はこの数は無限に大きくなりますが,その増加が極めて遅い代表例です。このことが納得できるのは大学1年程度の数学の知識が必要です。皆さんの今後の勉強に委ねます。

|
買い物に自動車で出かけたAさんは,制限速度が時速40Kmの道を時速60kmで走っていました。 するとパトカーに制止されて,お巡りさんに注意を受けました。「この道の制限速度は時速40kmですよ。 あなたは今時速60kmで走っていましたので違反です。」
するとAさんは「そんなはずはありません。私は家を出てまだ5分しかたっていません。」 |
自動車には速度計が付いていて,刻々の速度を表示しています。さて,速度というものは[移動した距離]/[かかった時間]で計算しますが,
瞬間の速度はどうやって測るのでしょうか。
上の小咄のように,1時間経って40km移動すれば時速40kmであることは明白ですが,ある瞬間に
時速40kmである,ということを理解するには若干の準備とそれなりの手順が必要です。ここではその手順を考えてみましょう。


|
下のアニメーションをご覧下さい。時刻t=10秒における速度を求めるには次のような手続きをします。
|

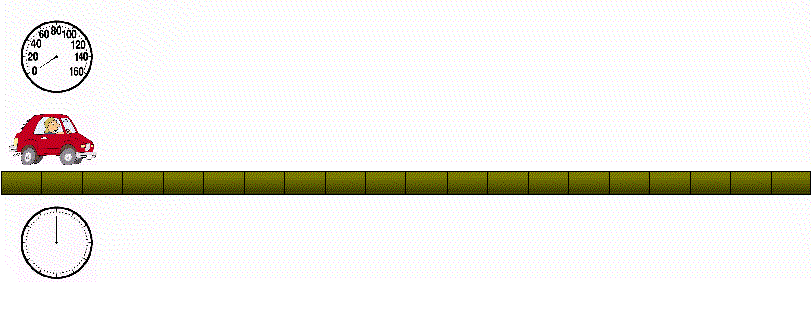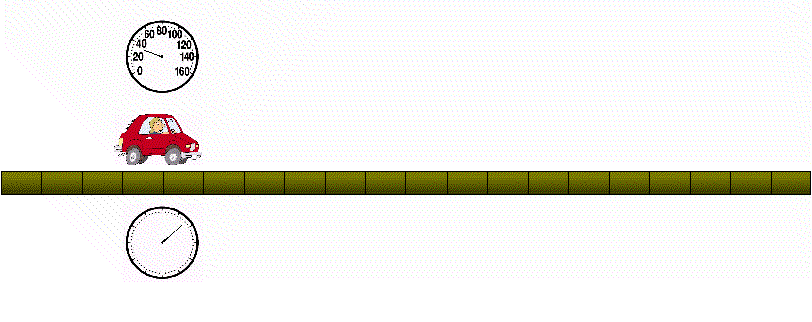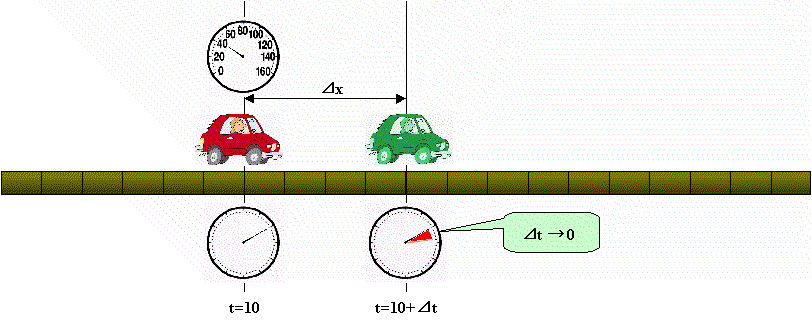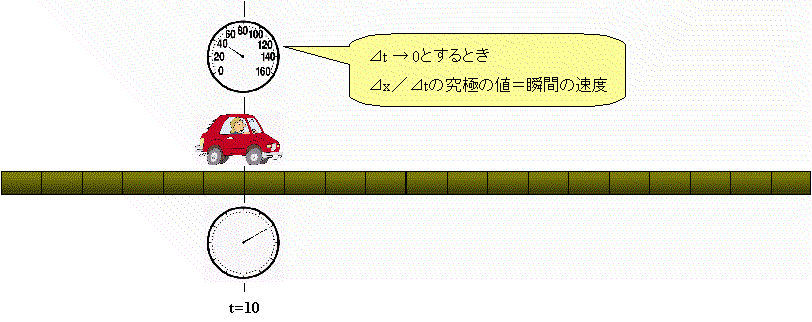
|
自動車の位置xは出発点から最終点に向かって時間と共に変化していきますから,時間の関数としてx(t)と書くことにします。
それに伴う速度v(t)は,時速0kmから時速60kmまで変化しながら,最終点で停止します。
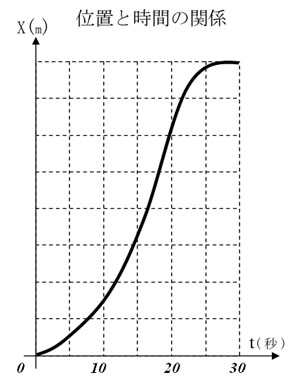
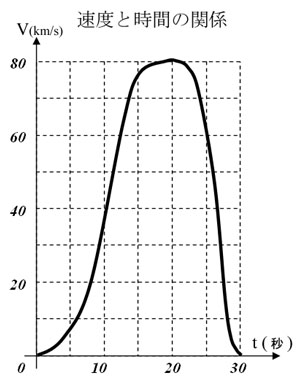
グラフ上で上と同様の微分という操作をしてみましょう。
|

|
まとめると,
時刻t=10秒での瞬間の速度は,位置を表す関数のA点での接線の傾きを表している ということです。
さてここまでくると,ゼノンの逆説「飛んでる矢は止まっている」の答えが見えてきたのではありませんか。
瞬間という意味は,そこでは時間の間隔は0ですが,初めから0で議論をするのではなく,暫定的な 仮想の間隔⊿tを想定して議論し,その⊿tを限りなく0に近づけた極限でもって瞬間を理解しています。
従って,自動車も矢も動いているものは,その瞬間において速度を持っています。
この状況を「動いている」というのか,「静止している」というのかは,言葉の定義の問題になりますから軽々しくは結論できません。しかし
極限の操作を了解した上では,瞬間においても動いている
と考えた方がよいと思います。(数学では「無限小の時間間隔に無限小の移動がある」,というような理解の仕方をすることがあります。)
さて少し一般的な議論を進めてみましょう。
変化していく量を表現する巧みな方法として,関数で表現する方法があります。つまり,xが変化するとき,それにともなってyが変化していく関係「y=f(x)」を関数といいますね。この関係を,例えばy=2x+3とかy=x2-2x+3というように関係を式で表現したり,グラフを書くことによって視覚的に理解したりします。
関数をグラフで表現して,このグラフ上をxが変化するとき,「このグラフは瞬間的にどのように変化していると言えばよいか」を議論してみましょう。
考えていく手順は速度の場合と全く同じです。まず,グラフ上のある点A(x,y)において,そこから少し行った点Bをとり,線分ABの傾きをもって,近似的にグラフのAB間の変化であるとします。次にBをAに次第に(無限に)近づけていけば,線分ABの傾きは究極的に(極限として),点Aでのグラフの変化の方向と見なせる訳です。
グラフ上の点xにおける瞬間のグラフの傾きを微分係数といいます。微分係数は,xが変化すれば刻々と変化します。従ってその微分係数もxの関数とみなせます。この関数を導関数といい,もとの関数の名前がfならばその導関数はf’で表します。元の関数からその導関数を求めることを「微分する」といいます。
まとめると
導関数とは,元の関数から派生した関数であり,元の関数のグラフ上の刻々の傾きを表したもの
ということです。
では今のことを実際のグラフで体感してみましょう。
【操作方法】
|
どうでしたか。滑らかに曲がっているグラフ上の,瞬間々の変化の方向(傾き)が感じ取れましたか。
さて次に,関数のグラフにおける瞬間の傾きから導関数の描いてみましょう。
関数とその導関数の関係が分かりましたか。
関数が分かれば導関数は導出できるし,導関数が分かれば元の関数が想像できます。 関数とその導関数の関係はちょうど親子関係のようであり,「この親にしてこの子あり」とか「親の顔が見たい」といった状況は,関数の世界でも常に起こります。
さてその「親の顔が見たい」という欲求は,関数においては導関数からその元になっている関数を想像しようという欲求に対応します。
導関数から元の関数を求める操作を「積分する」といいます。 ですから,「微分する」という操作と「積分する」という操作は,ちょうど逆の操作ということになります。

このことを数学の記号で表現すると,

となります。ここで,df(x)/dxとはf(x)を微分した関数(すなわち導関数),∫f(x)dxとは微分するとf(x)となるような関数(すなわち原始関数又は不定積分)という意味の記号です。
この記号の由来は,それぞれ「微分する」「積分する」という操作をイメージ化したものです。
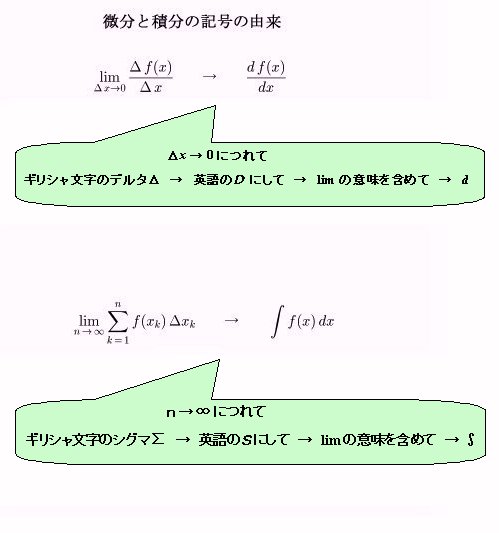
従って,導関数のdf(x)/dxを見ると,グラフ上の点におけるxの瞬間の増分△xとyの瞬間の増分△yの比の極限状態をイメージしているし,原始関数の∫f(x)dxを見ると,f(x)の値とxの瞬間の増分の積の寄せ集めをイメージしています。
さて,「微分する」ことと「積分する」ことは逆の操作でしたので,行ったり来たりできる操作ですが,一つ注意が必要です。それは定数を微分すると0になってしまいますから,微分した後積分すると定数分の情報が失われてしまうということです。言い換えると,
積分するときには,定数分だけの任意性(一通りに決められないという性質)が生じる
ということになります。具体的な関数における微分積分の対照関係をご覧下さい。
では次に,その「積分する」ことの意味をもう少し詳しくみていきましょう。
「積分する」ということは,「微分する」ことの逆の操作であることはすでにみてきましたが,次のように考えることが「積分する」ことをイメージするのに有効です。
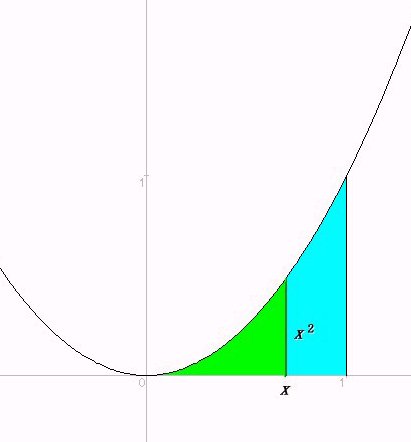
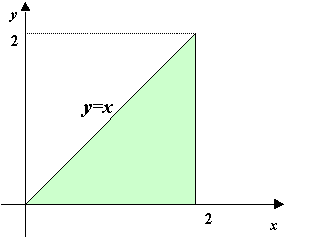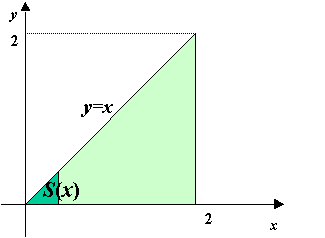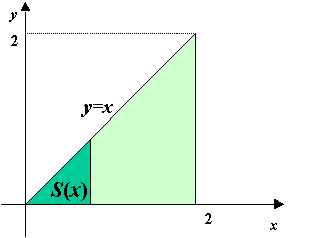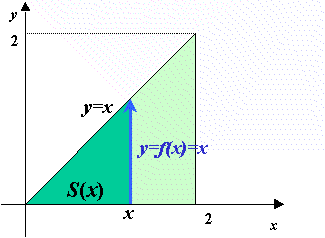
まずy=f(x)(ただし,x>0でf(x)>0とします。)を考えます。そして,そのf(x)とx軸との間にできる図形の面積をS(x)とし,S(x)がどのように増加していくかを考えます。
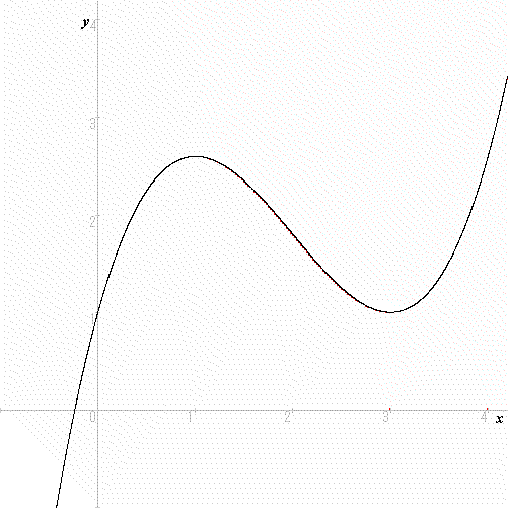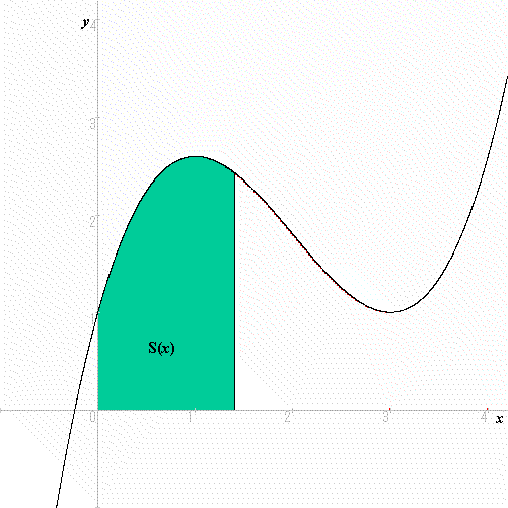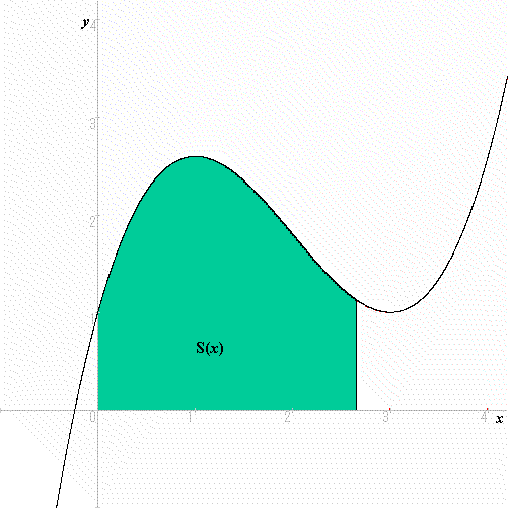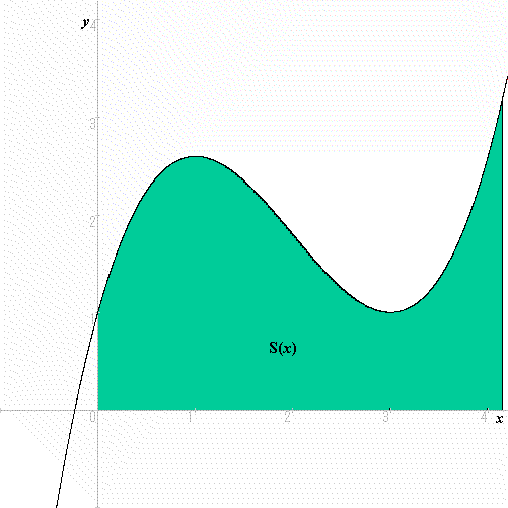
さて,この面積S(x)は,瞬間にどれだけ増加しているのでしょうか。瞬間に増える量を表現する記号は,dS(x)/dxでしたね。よく考えてみてください。
そうです。このように,S(x)が瞬間に増加する量はf(x)なのです。つまり,
dS(x)/dx=f(x)
ということです。従って,f(x)はS(x)の導関数であり,S(x)はf(x)を積分したもの(不定積分,又は原始関数)であることになります。
さて,具体的な関数を例にして,S(x)を求めてみましょう。
関数f(x)=x2(0≦x≦1)の下にできる図形の面積を求めてみます。
上での議論のように,dS/dx=x2ですから,S(x)はx2を積分すればよいことになりますね。
 |
 |
さていままでのことをまとめると,
ということになります。
(だたし,x≧0でf(x)≧0という条件がつきます。)
この問題は17・18世紀にニュートン・ライプニッツ 等によって確立された「微分積分学」によって理解できるようになりました。これは人類にとっての大きな遺産です。これによって現代の科学技術が支えられているといっても過言ではありません。
さて「瞬間を捉える」というアイデアの凄さを,図形の面積や体積を求めることを通してみていきましょう。
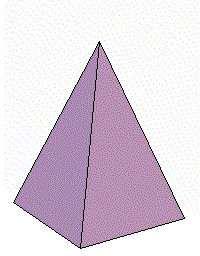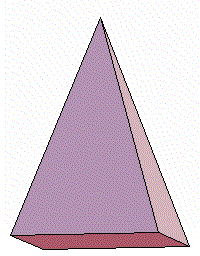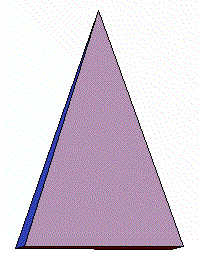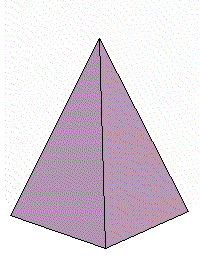
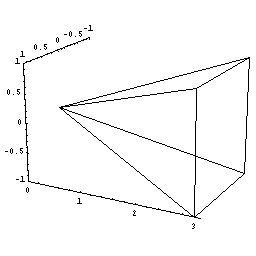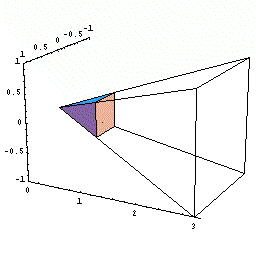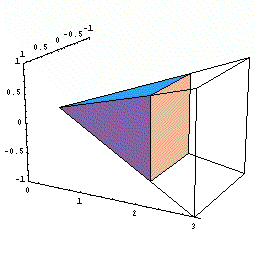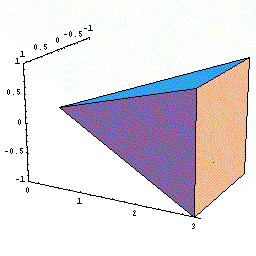
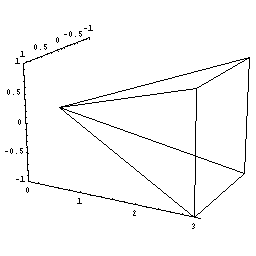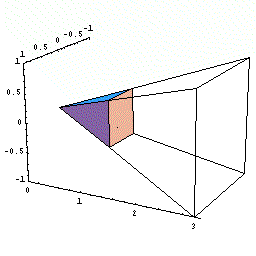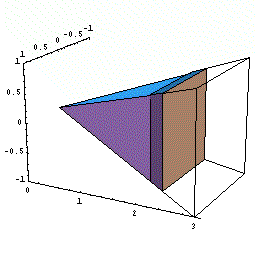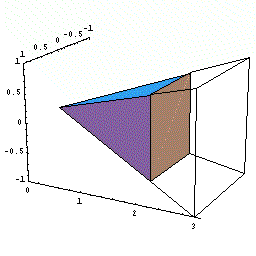
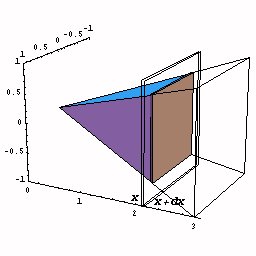
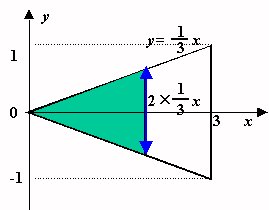
まず直角二等辺三角形の面積を求めてみましょう。
三角形面積は底辺×高さ÷2ですからすぐに求まりますが,微分積分のアイデアを使うと次のようになります。
|
|

|
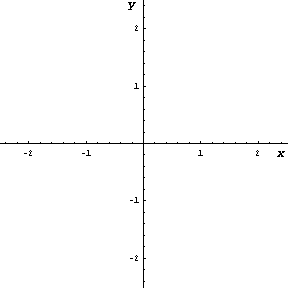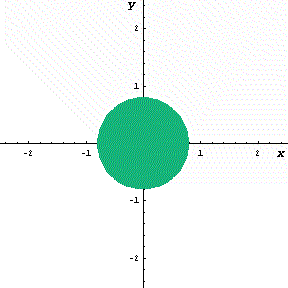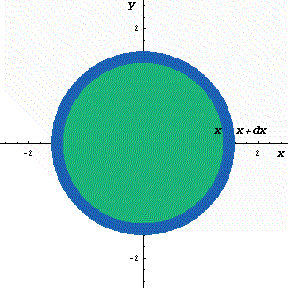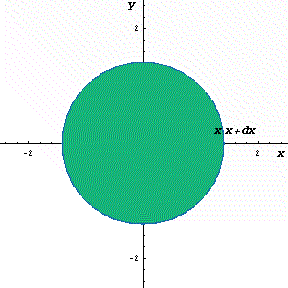
|
|
|
|
|
|

|
|
次に,やはり対称性のよい図形として回転体の体積を議論してみましょう。
下図のように,y=f(x)=2x(x-1)2=2x3ー4x2+2x(0≦x≦1.5)をx軸の周りに回転してできる図形を考えます。
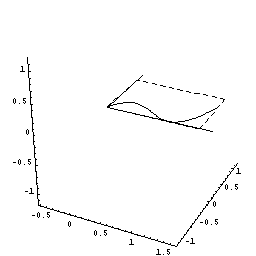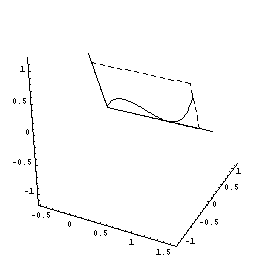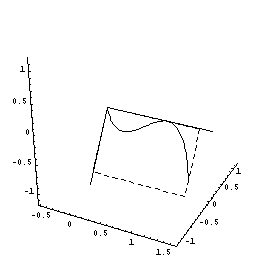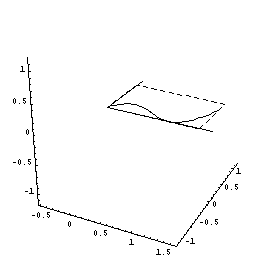
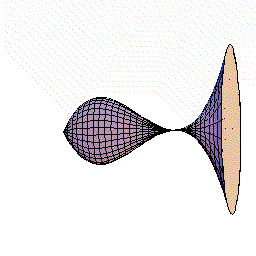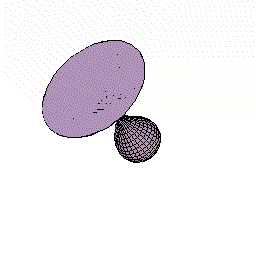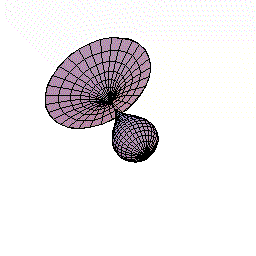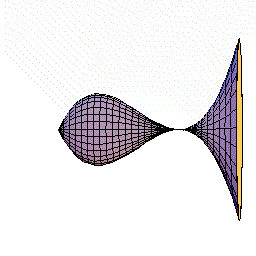
さてこの立体を,回転軸のxの位置で,軸に垂直に切断すると,0からxまでにできた立体V(x)が瞬間に増加する量は,その切断面の面積分であることがわるでしょう。
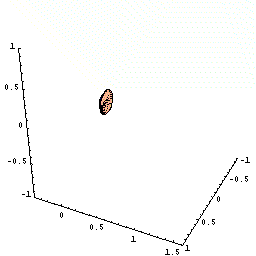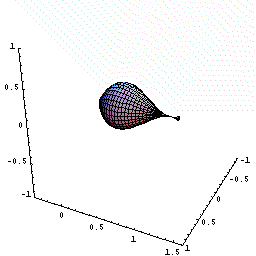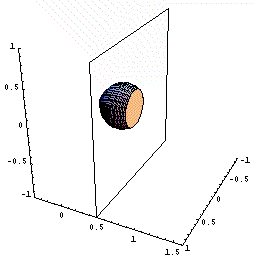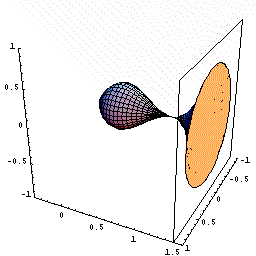
しかも,その切断面は半径がf(x)=2x(x-1)2の円ですね。
従って,dV/dx=π{f(x)}2であることも,もうわかりましたね。
|

|