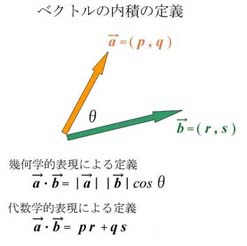
幾何学的表現と代数学的表現による定義は、
結果的に同じもの(同値)
2つのベクトルのかけ算は、内積と外積の2つが定義されています。 ここでは内積について、その考え方をみていきましょう。
実は、内積の定義を聞いても、そんなにワクワクドキドキするようなものではないかもしれません。
でもまずは、内積の定義を述べましょう。

|
|
これらの定義をみると、「どうしてそのように定義するのか?」という疑問がさらに湧いてくるのではないでしょうか。
この疑問に答えることはかなり厄介です。というのは、このように内積を定義する必然性は、私たちの日常的感覚からくるというよりむしろ、数学という学問そのものの「内なる要請」からきている傾向が強いように(私は)思います。
すなわち、
|
このように定義すると、
|
というわけですが、正直言って、このような説明を聞いても、なかなか腹に落ちて納得できるものではありませんね。
とは言うものの、「数学上の都合」を垣間見るいくつかの例を見ていくことにしましょう。
物理を勉強していく中で、
「(働いた力の大きさ)×(移動距離)を仕事といい、仕事をする能力をエネルギーという。・・・」ことを学びます。
次の例でこの「仕事」を計算してみましょう。
質量2kgのボールが3m落下しました。このとき、重力のした仕事は、2×3=6(ジュール)です。
この場合、単純な数値どうしのかけ算で済みます。これは、働いた重力の向きと移動したボールの方向が同じだからです。
しかし、日常目につく落下運動は、もっと複雑です。
すなわち、重力は大きさと向きを持つベクトル量であることは言うまでもありませんが、物体はそれが斜面に置かれているとか、束縛されたレールに沿って動くなど、移動方向も様々であり、移動も、距離とその方向を持つベクトルと考える必要があります。この移動は、専門用語では「変位」と呼ぶこともあります。
次の例をみましょう。
|
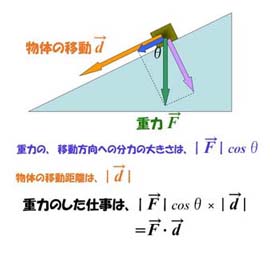
|
このようなわけで、この内積を使えば「仕事=変位ベクトル・力ベクトル」というように、簡潔で美しい表現となります。
あるスーパーマーケットでは、にんじんが1本30円で売っているとします。Aさんがにんじんを4本買いました。さて、いくらになるでしょうか。
この問題は簡単ですね。金額=単価×個数ですから、30×4=120(円)です。
このような状況を、次のように拡張して考えていきましょう。
|
「購入金額=それぞれの野菜の(単価×個数)の和」となり、
|
こうすることにより、内積の代数学的定義を、「購入金額=単価ベクトル・個数ベクトル」のように、簡潔で美しい表現とすることができます。
複数の数値をセットとしたものをベクトルとしましたが、さらに拡張して考えて、複数のベクトルをセットとしたものを議論しましょう。
数字を縦横に並べて長方形状にし、それを一つのセットとみたものを行列といいます。
その拡張していく過程の中で、内積が果たす役割に注目してください。
|
このように、行列は複数のベクトルをセットにしたものと見なすことができます。
さて、行列どうしの演算を考えてみましょう。行列はベクトルの拡張ですから、ベクトルの和差積の感覚がそのまま拡張されます。
|

|
さて次に、行列どうしの積を考えましょう。積は、内積の拡張と考えます。
すなわち、
|
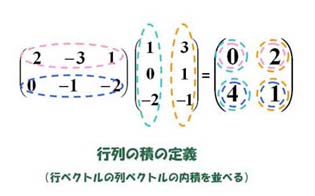
|
このような行列と行列の積を用いると、表現上あるいは概念形成上、便利なことがいくつかあります。
その中の一つの例として、中学・高校で学んだ連立方程式を取り上げましょう。
|
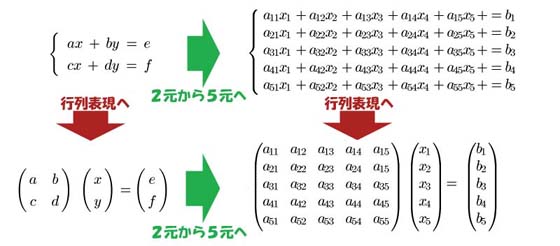
|
普通の数(スカラー量)から出発して、ベクトル、行列へと拡張していくとき、普通の数は1×1行列、ベクトルは行ベクトルなら1×m行列、列ベクトルならm×1行列というように、今までの概念を内包しつつ、しかも演算の法則も保存されるように拡張していきます。このようにして、拡張する前と後で同じ考え方が貫き通され、単純で統一的な体系としてまとめられます。

一方かけ算については、2×3=3×2、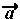 ・
・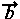 =
=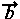 ・
・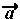 であり、演算の前後で交換可能ですが、行列ではAB≠BAであり交換不可となります。これにより新たな事態が生じます。
であり、演算の前後で交換可能ですが、行列ではAB≠BAであり交換不可となります。これにより新たな事態が生じます。
これは困った事態というよりむしろ、そのような交換不可能な演算も同じ仲間として受け入れ、
より柔軟に思考できる新しい世界が拓けた
と見るべきでしょう。
ここに数学の美学の一端を垣間見ることができるでしょう。
今までみてきたように、ベクトルの内積の定義は、「数学などの学問上の内なる要請」が色濃く反映しているため、日常的な感覚からは、わかりにくいとか、形式ばっているとか、面倒であるといった印象が生じやすく、数学を敬遠する一因でもあるようです。
しかし、このことは数学に責任があるのではなく、むしろ、
身の回りの現象や対象物は、スカラー的ではなくベクトルや行列でないと表現できない程複雑なものが多くあり、数学はそれを解明しようと果敢に挑戦している
とみるべきでしょう。
内積を終えるに当たって、内積の計算練習や内積の感覚作りのために、
で、様々なベクトルどうしの内積を体験してみましょう。
