偝偰彮偟堦斒揑側媍榑傪恑傔偰傒傑偟傚偆丅
曄壔偟偰偄偔検傪昞尰偡傞岻傒側曽朄偲偟偰丆娭悢偱昞尰偡傞曽朄偑偁傝傑偡丅偮傑傝丆倶偑曄壔偡傞偲偒丆偦傟偵偲傕側偭偰倷偑曄壔偟偰偄偔娭學乽倷亖倖乮倶乯乿傪娭悢偲偄偄傑偡偹丅偙偺娭學傪丆椺偊偽倷亖俀倶亄俁偲偐倷亖倶俀亅俀倶亄俁偲偄偆傛偆偵娭學傪幃偱昞尰偟偨傝丆僌儔僼傪彂偔偙偲偵傛偭偰帇妎揑偵棟夝偟偨傝偟傑偡丅
娭悢傪僌儔僼偱昞尰偟偰丆偙偺僌儔僼忋傪倶偑曄壔偡傞偲偒丆乽偙偺僌儔僼偼弖娫揑偵偳偺傛偆偵曄壔偟偰偄傞偲尵偊偽傛偄偐乿傪媍榑偟偰傒傑偟傚偆丅
峫偊偰偄偔庤弴偼懍搙偺応崌偲慡偔摨偠偱偡丅傑偢丆僌儔僼忋偺偁傞揰俙乮倶丆倷乯偵偍偄偰丆偦偙偐傜彮偟峴偭偨揰俛傪偲傝丆慄暘俙俛偺孹偒傪傕偭偰丆嬤帡揑偵僌儔僼偺俙俛娫偺曄壔偱偁傞偲偟傑偡丅師偵俛傪俙偵師戞偵乮柍尷偵乯嬤偯偗偰偄偗偽丆慄暘俙俛偺孹偒偼媶嬌揑偵乮嬌尷偲偟偰乯丆揰俙偱偺僌儔僼偺曄壔偺曽岦偲尒側偣傞栿偱偡丅
僌儔僼忋偺揰倶偵偍偗傞弖娫偺僌儔僼偺孹偒傪旝暘學悢偲偄偄傑偡丅旝暘學悢偼丆倶偑曄壔偡傟偽崗乆偲曄壔偟傑偡丅廬偭偰偦偺旝暘學悢傕倶偺娭悢偲傒側偣傑偡丅偙偺娭悢傪摫娭悢偲偄偄丆傕偲偺娭悢偺柤慜偑倖側傜偽偦偺摫娭悢偼倖乫偱昞偟傑偡丅尦偺娭悢偐傜偦偺摫娭悢傪媮傔傞偙偲傪乽旝暘偡傞乿偲偄偄傑偡丅
傑偲傔傞偲
摫娭悢偲偼丆尦偺娭悢偐傜攈惗偟偨娭悢偱偁傝丆尦偺娭悢偺僌儔僼忋偺崗乆偺孹偒傪昞偟偨傕偺
偲偄偆偙偲偱偡丅
偱偼崱偺偙偲傪幚嵺偺僌儔僼偱懱姶偟偰傒傑偟傚偆丅
亂憖嶌曽朄亃
|
偳偆偱偟偨偐丅妸傜偐偵嬋偑偭偰偄傞僌儔僼忋偺丆弖娫乆偺曄壔偺曽岦乮孹偒乯偑姶偠庢傟傑偟偨偐丅
偝偰師偵丆娭悢偺僌儔僼偵偍偗傞弖娫偺孹偒偐傜摫娭悢偺昤偄偰傒傑偟傚偆丅
娭悢偲偦偺摫娭悢偺娭學偑暘偐傝傑偟偨偐丅
娭悢偑暘偐傟偽摫娭悢偼摫弌偱偒傞偟丆摫娭悢偑暘偐傟偽尦偺娭悢偑憐憸偱偒傑偡丅 娭悢偲偦偺摫娭悢偺娭學偼偪傚偆偳恊巕娭學偺傛偆偱偁傝丆乽偙偺恊偵偟偰偙偺巕偁傝乿偲偐乽恊偺婄偑尒偨偄乿偲偄偭偨忬嫷偼丆娭悢偺悽奅偱傕忢偵婲偙傝傑偡丅
偝偰偦偺乽恊偺婄偑尒偨偄乿偲偄偆梸媮偼丆娭悢偵偍偄偰偼摫娭悢偐傜偦偺尦偵側偭偰偄傞娭悢傪憐憸偟傛偆偲偄偆梸媮偵懳墳偟傑偡丅
摫娭悢偐傜尦偺娭悢傪媮傔傞憖嶌傪乽愊暘偡傞乿偲偄偄傑偡丅 偱偡偐傜丆乽旝暘偡傞乿偲偄偆憖嶌偲乽愊暘偡傞乿偲偄偆憖嶌偼丆偪傚偆偳媡偺憖嶌偲偄偆偙偲偵側傝傑偡丅

偙偺偙偲傪悢妛偺婰崋偱昞尰偡傞偲丆

偲側傝傑偡丅偙偙偱丆倓倖乮倶乯乛倓倶偲偼倖乮倶乯傪旝暘偟偨娭悢乮偡側傢偪摫娭悢乯丆佺倖乮倶乯倓倶偲偼旝暘偡傞偲倖乮倶乯偲側傞傛偆側娭悢乮偡側傢偪尨巒娭悢枖偼晄掕愊暘乯偲偄偆堄枴偺婰崋偱偡丅
偙偺婰崋偺桼棃偼丆偦傟偧傟乽旝暘偡傞乿乽愊暘偡傞乿偲偄偆憖嶌傪僀儊乕僕壔偟偨傕偺偱偡丅
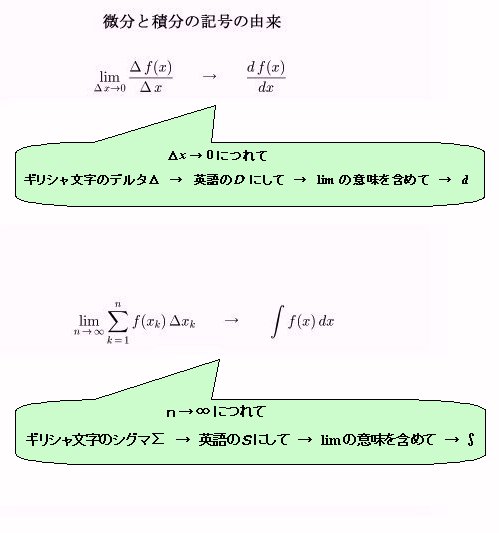
廬偭偰丆摫娭悢偺倓倖乮倶乯乛倓倶傪尒傞偲丆僌儔僼忋偺揰偵偍偗傞倶偺弖娫偺憹暘仮倶偲倷偺弖娫偺憹暘仮倷偺斾偺嬌尷忬懺傪僀儊乕僕偟偰偄傞偟丆尨巒娭悢偺佺倖乮倶乯倓倶傪尒傞偲丆倖乮倶乯偺抣偲倶偺弖娫偺憹暘偺愊偺婑偣廤傔傪僀儊乕僕偟偰偄傑偡丅
偝偰丆乽旝暘偡傞乿偙偲偲乽愊暘偡傞乿偙偲偼媡偺憖嶌偱偟偨偺偱丆峴偭偨傝棃偨傝偱偒傞憖嶌偱偡偑丆堦偮拲堄偑昁梫偱偡丅偦傟偼掕悢傪旝暘偡傞偲侽偵側偭偰偟傑偄傑偡偐傜丆旝暘偟偨屻愊暘偡傞偲掕悢暘偺忣曬偑幐傢傟偰偟傑偆偲偄偆偙偲偱偡丅尵偄姺偊傞偲丆
愊暘偡傞偲偒偵偼丆掕悢暘偩偗偺擟堄惈乮堦捠傝偵寛傔傜傟側偄偲偄偆惈幙乯偑惗偠傞
偲偄偆偙偲偵側傝傑偡丅嬶懱揑側娭悢偵偍偗傞旝暘愊暘偺懳徠娭學傪偛棗壓偝偄丅
偱偼師偵丆偦偺乽愊暘偡傞乿偙偲偺堄枴傪傕偆彮偟徻偟偔傒偰偄偒傑偟傚偆丅
乽愊暘偡傞乿偲偄偆偙偲偼丆乽旝暘偡傞乿偙偲偺媡偺憖嶌偱偁傞偙偲偼偡偱偵傒偰偒傑偟偨偑丆師偺傛偆偵峫偊傞偙偲偑乽愊暘偡傞乿偙偲傪僀儊乕僕偡傞偺偵桳岠偱偡丅
傑偢倷亖倖乮倶乯乮偨偩偟丆倶亜侽偱倖乮倶乯亜侽偲偟傑偡丅乯傪峫偊傑偡丅偦偟偰丆偦偺倖乮倶乯偲倶幉偲偺娫偵偱偒傞恾宍偺柺愊傪俽乮倶乯偲偟丆俽乮倶乯偑偳偺傛偆偵憹壛偟偰偄偔偐傪峫偊傑偡丅
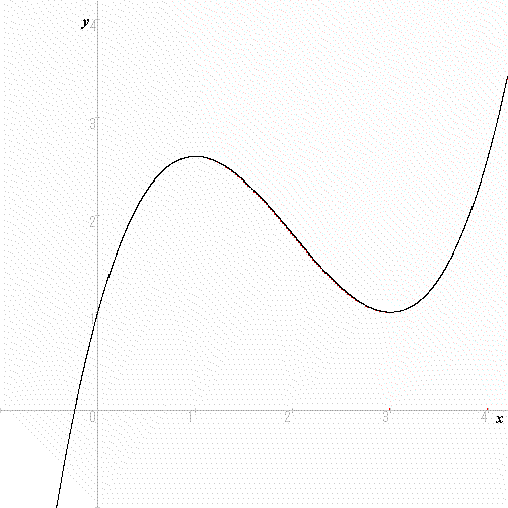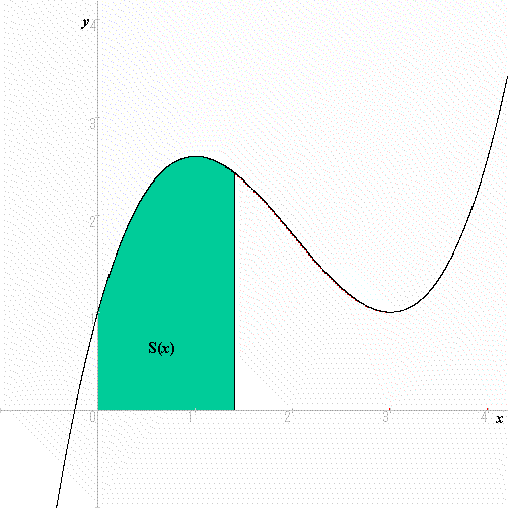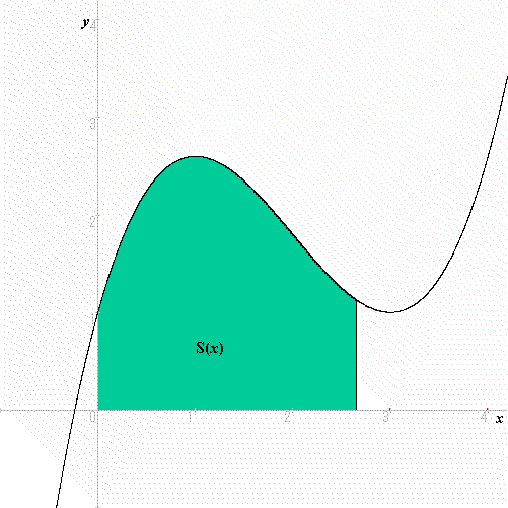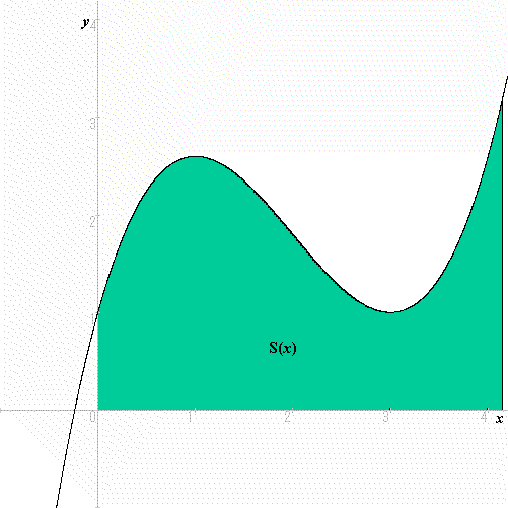
偝偰丆偙偺柺愊俽乮倶乯偼丆弖娫偵偳傟偩偗憹壛偟偰偄傞偺偱偟傚偆偐丅弖娫偵憹偊傞検傪昞尰偡傞婰崋偼丆倓俽乮倶乯乛倓倶偱偟偨偹丅傛偔峫偊偰傒偰偔偩偝偄丅
偦偆偱偡丅偙偺傛偆偵丆俽乮倶乯偑弖娫偵憹壛偡傞検偼倖乮倶乯側偺偱偡丅偮傑傝丆
倓俽乮倶乯乛倓倶亖倖乮倶乯
偲偄偆偙偲偱偡丅廬偭偰丆倖乮倶乯偼俽乮倶乯偺摫娭悢偱偁傝丆俽乮倶乯偼倖乮倶乯傪愊暘偟偨傕偺乮晄掕愊暘丆枖偼尨巒娭悢乯偱偁傞偙偲偵側傝傑偡丅
偝偰丆嬶懱揑側娭悢傪椺偵偟偰丆俽乮倶乯傪媮傔偰傒傑偟傚偆丅
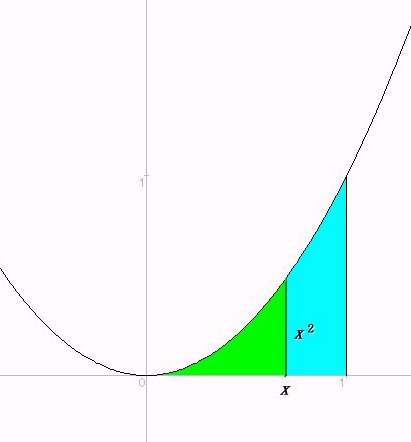
娭悢倖乮倶乯亖倶俀乮侽亝倶亝侾乯偺壓偵偱偒傞恾宍偺柺愊傪媮傔偰傒傑偡丅
忋偱偺媍榑偺傛偆偵丆倓俽乛倓倶亖倶俀偱偡偐傜丆俽乮倶乯偼倶俀傪愊暘偡傟偽傛偄偙偲偵側傝傑偡偹丅
 |
 |
偝偰偄傑傑偱偺偙偲傪傑偲傔傞偲丆
偲偄偆偙偲偵側傝傑偡丅
丂
乮偩偨偟丆倶亞侽偱倖乮倶乯亞侽偲偄偆忦審偑偮偒傑偡丅乯
